PRAVILNIK O PROGRAMU ZAVRŠNOG ISPITA U OSNOVNOM OBRAZOVANJU I VASPITANJU("Sl. glasnik RS - Prosvetni glasnik", br. 1/2011, 1/2012, 1/2014, 12/2014, 2/2018, 3/2021, 14/2022, 4/2023 i 5/2023 - ispr.) |
Követelményrendszer a kötelező oktatás végére matematikából, megadott minta feladatokkal
МА.1.1.1. A tanuló tudja a különböző típusú számokat elolvasni és leírni (természetes, egész, racionális)
Feladat |
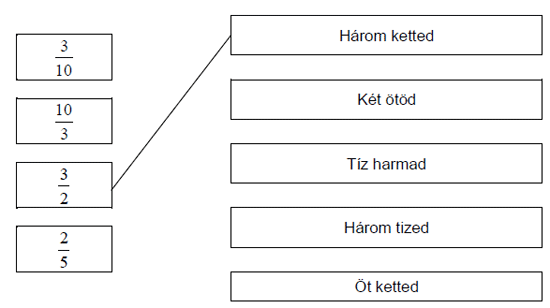
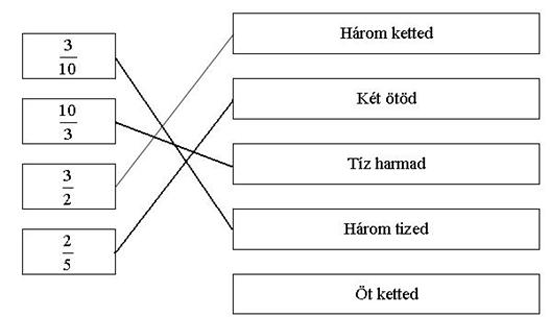
Kösd össze vonallal az egyenlő számokat hasonlóképpen, mint ahogy elkezdtük:
|
Megoldás |
|
МА.1.1.2. A tanuló tudja a tizedes törtet átalakítani törtté és fordítva.
Feladat |
A felkínált számok közül melyik egyenlő a 0,3 számmal? Karikázd be a helyes válasz előtti betűt. a) 10/3 b) 3/10 c) 1/3 d) 3/1 |
Megoldás |
b) 3/10 |
МА.1.1.3. A tanuló tudja az ugyanolyan alakban felírt számokat nagyság szerint összehasonlítani, szükség esetén rajz segítségével.
Feladat |
|||||||||
Adottak a következő számok:
|
|||||||||
|
|||||||||
Megoldás |
|||||||||
|
МА.1.1.4. A tanuló tudja ugyanolyan alakban felírt számok között az alapműveleteket elvégezni, szükség esetén rajz segítségével (törtek összeadása és kivonása esetén csak közös nevezőjű törtekkel); tudja például az n 1/5 részét kiszámolni, ahol n adott természetes szám.
Feladat |
Végezd el a műveletet és írd fel a megfelelő eredményt: a) - 6 : 2 = ________ b) - 6 - 2 = ________ c) - 6 ∙ 2 = ________ d) - 6 + 2 = ________ |
Megoldás |
a) - 6 : 2 = −3 b) - 6 - 2 = −8 c) - 6 ∙ 2 = −12 d) - 6 + 2 = −4 |
МА.1.1.5. A tanuló tud egyjegyű számmal maradékosan osztani és tudja, hogy egy szám mikor osztható egy másikkal.
Feladat |
||||||||||||||||||
Töltsd ki a következő táblázatot az elkezdett módon:
|
||||||||||||||||||
Megoldás |
||||||||||||||||||
|
МА.1.1.6. A tanuló tudja használni az egész számokat és a velük kapcsolatos egyszerűbb kifejezéseket vizuális ábrázolás segítségével.
Feladat |
Julcsi, akinek ma van a születésnapja, így szólt: Karikázd be a helyes válasz előtti betűt. а) 12 b) 15 c) 18 d) 21 |
Megoldás |
b) 15 |
МА.1.2.1. A tanuló tudja a leegyszerűsített és interpretációtól függő formális műveleteket elvégezni; képes olyan lineáris egyenleteket megoldani, amelyekben az ismeretlen csak egy tagban fordul elő.
Feladat |
Melyik szám az x/2 + 2 = 8 egyenlet megoldása? Karikázd be a helyes válasz előtti betűt. а) 5 b) 6 c) 12 d) 20 |
Megoldás |
c) 12 |
МА.1.2.2. A tanuló tudja a leegyszerűsített és interpretációtól függő formális műveleteket elvégezni; képes adott szám hatványát kiszámolni, tudja a hatványokkal kapcsolatos alapműveleteket.
Feladat |
Karikázd be a helyes válasz előtti betűt. A 210 • 22 szorzat felírható, mint: а) 25 b) 28 c) 212 d) 220 |
Megoldás |
c) 212 |
Feladat |
Karikázd be a helyes válasz előtti betűt. а) 0,06 b) 0,6 c) 0,09 d) 0,9 |
Megoldás |
c) 0,09 |
МА.1.2.3. A tanuló tudja a leegyszerűsített és interpretációtól függő formális műveleteket elvégezni; képes egytagú kifejezéseket (monomokat) összeadni, kivonni és szorozni.
Feladat |
Rendezd a következő kifejezéseket: 5a3 + 7a3 = _______ 9x2 - 4x2 = _______ 2b • 3b2 = _______ |
Megoldás |
5a3 + 7a3 = 12a3 9x2 - 4x2 = 5x2 2b • 3b2 = 6b3. |
МА.1.2.4. A tanuló tudja a leegyszerűsített és interpretációtól függő formális műveleteket elvégezni; képes a táblázattal vagy képlettel megadott függvény adott helyen felvett értékét meghatározni.
Feladat |
|||||||||||
A függvény az y = 2x + 1 formulával adott. Határozd meg az x és y változók mefelelő értékeit és töltsd ki a táblázatot.
|
|||||||||||
Megoldás |
|||||||||||
|
МА.1.3.1. A tanuló ismerje a: szakasz, félegyenes, egyenes, sík és szög fogalmát (felismerje azok modelljeit a valós világban és tudja őket megfelelő eszközök segítségével lerajzolni; tudja megkülönböztetni az egyes szögfajtákat, valamint a párhuzamos és merőleges egyeneseket).
Feladat |
Kösd össze a képet a képen látható alakzat nevével.
|
Megoldás |
|
МА.1.3.2. A tanuló ismerje a: háromszög, négyszög, négyzet és téglalap fogalmát (felismerje azok modelljeit a valós világban és tudja őket megfelelő eszközök segítségével lerajzolni; a tanuló tudja megkülönböztetni a háromszögek alapvető fajtáit, ismerje a háromszög alapvető alkotóelemeit és tudja a háromszög, négyzet és téglalap kerületét és területét kiszámolni a feladatban közvetlenül megadott adatok alapján; tudja a derékszögű háromszög ismeretlen oldalát kiszámolni a Pitagorasz tétel segítségével).
Feladat |
Mekkora területet fed be a padlón a 3,5 m hosszúságú és 2 m szélességű szőnyeg? Karikázd be a helyes válasz előtti betűt: а) 11 m2 b) 7 m2 c) 5,5 m2 d) 3,5 m2 |
Megoldás |
b) 7 m2 |
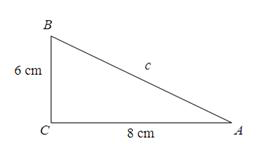
Feladat |
||
Számold ki a képen látható derékszögű háromszög átfogóját.
|
||
Megoldás |
||
c = 10 cm |
МА.1.3.3. A tanuló ismerje a: kör, körvonal fogalmát (tudja alapvető alkotóelemeiket megkülönböztetni, felismerje azok modelljeit a valós világban és tudja őket megfelelő eszközök segítségével lerajzolni; tudja adott sugarú kör kerületét és területét kiszámolni).
Feladat |
Mekkora annak a körnek kerülete, amelynek sugara 7 cm? Karikázd be a helyes válasz előtti betűt. а) 14 cm b) 49 cm c) 14p cm d) 49p cm |
Megoldás |
c) 14p cm |
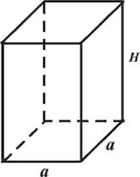
МА.1.3.4. A tanuló ismerje a: kocka és téglatest fogalmát (felismerje azok modelljeit a valós világban, ismerje azok alkotóelemeit és tudja felszínüket és térfogatukat kiszámolni).
Feladat |
A szabályos négyoldalú hasáb alapéle 6 cm, a hasáb magassága pedig 10 cm. Mekkora az adott hasáb felszíne?
A hasáb felszíne ___________ cm2. |
Megoldás |
F = 2 • 36 cm2 + 4 • 60 cm2 = 312 cm2 A hasáb felszíne 312 cm2. |
МА.1.3.5. A tanuló ismerje a: kúp, henger és gömb fogalmát (felismerje azok modelljeit a valós világban, ismerje azok alkotóelemeit).
Feladat |
Minden hengerre írd rá az 1-es számot, minden kúpra a 2-es számot, és minden gömbre a 3-as számot.
|
| Megoldás |
|
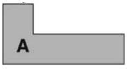
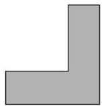
МА.1.3.6. A tanuló tudja az egybevágó alakzatokat felismerni (lefedésig való elmozgatással).
Feladat |
||||||
|
||||||
Megoldás |
||||||
c)
|
Feladat |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Adott az F alakzat. Fesd be a szükséges részt úgy, hogy a G alakzat egybevágó legyen (lefedhető legyen) az F alakzattal.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Megoldás |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
МА.1.4.1. A tanuló tudja a megfelelő mértékegységeket használni a hosszúság, terület, térfogat, tömeg, idő és szög mérésére.
Feladat |
|||||||||||||||
Töltsd ki a táblázat üres helyeit a megfelelő mértékegységekkel.
|
|||||||||||||||
Megoldás |
|||||||||||||||
|
МА.1.4.2. A tanuló tudja a nagyobb hosszúság, tömeg és idő mértékegységeket kisebbekké átalakítani.
Feladat |
Melyik időtartam a leghosszabb? Karikázd be a helyes válasz előtti betűt. а) három hónap b) 100 nap c) 10 hét d) egy negyedév |
Megoldás |
b) 100 nap |
МА.1.4.3. A tanuló tudja a különböző váltópénzeket használni.
Feladat |
Ha 3 darab 200 dináros bankjegyet felváltasz 50 dináros bankjegyekre, akkor hány darab bankjegyet fogsz kapni?
______ darab 50 dináros bankjegyet fogok kapni. |
Megoldás |
12 darab 50 dináros bankjegyet fogok kapni. |
МА.1.4.4. A tanuló tudja a mérés során a megfelelő mértékegységet kiválasztani; tudja az adott mértékegységben kiszámolt értéket kerekíteni.
Feladat |
||||||||||||||||||
Írd be az üres helyre a megfelelő mértékegységet: km, cm, l, kg vagy g.
|
||||||||||||||||||
Megoldás |
||||||||||||||||||
|
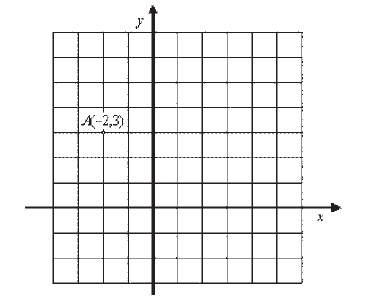
МА.1.5.1. A tanuló tudja az objektumok helyzetét sorokba és oszlopokba rendezve kifejezni; tudja a pont helyzetét meghatározni a koordinátarendszer első síknegyedében, ha adottak a pont koordinátái és fordítva.
Feladat |
A képen az ODEON mozi ülőhelyeinek alaprajza látható. Marci a hatodik sorban, bal oldalon a 3-as ülőhelyre kapott jegyet. Fesd be (satírozd be) Marci ülőhelyét.
|
Megoldás |
|
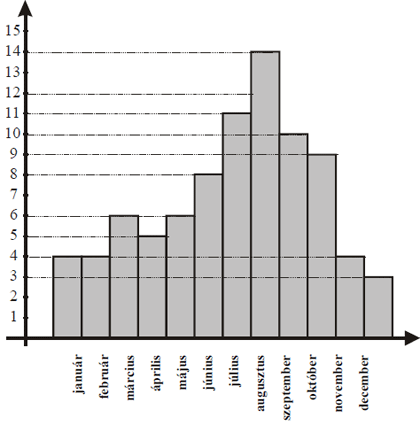
МА.1.5.2. A tanuló tudja a grafikonról, diagrammról vagy táblázatból az adatokat leolvasni, tudja őket értelmezni és tudja a függő mennyiség minimumát vagy maximumát meghatározni.
Feladat |
A napsütéses napok száma egy évben havi felbontásban a következő diagramon látható:
|
a) Legkevesebb napsütéses nap az év ___________ hónapjában volt. b) Legtöbb napsütéses nap az év ___________ hónapjában volt. |
Megoldás |
a) Legkevesebb napsütéses nap az év december hónapjában volt. b) Legtöbb napsütéses nap az év augusztus hónapjában volt. |
МА.1.5.3. A tanuló tudja a táblázat adatait grafikonnal ábrázolni és fordítva.
Feladat |
||||||||||||||
A tanulók írásbeli vizsgán való teljesítményének táblázata segítségével
fejezd be a következő grafikont ugyanolyan módon, mint ahogy elkezdtük.
|
||||||||||||||
Megoldás |
||||||||||||||
|
|
||||||||||||||
МА.1.5.4. A tanuló tudja egy mennyiség előfordulásának adott százalékát meghatározni.
Feladat |
Marika elhatározta, hogy vesz egy 4000 dináros tornacipőt. A vásárlás során 10% kedvezményt kapott az eladótól. Mennyi ez a kedvezmény dinárban kifejezve?
Marika ______ dinár kedvezményt kapott. |
Megoldás |
Marika 400 dinár kedvezményt kapott. |
МА.2.1.1. A tanuló tudja a különböző alakban felírt számokat nagyság szerint összehasonlítani.
Feladat |
|||||||
Adottak a következő számok:
Az adott számok közül melyik a legkisebb, és melyik a legnagyobb? A legkisebb szám ________, а legnagyobb szám pedig _______. |
|||||||
Megoldás |
|||||||
A legkisebb szám -1,2, а legnagyobb szám pedig 1½.. |
МА.2.1.2. A tanuló tudja az ellentett számot, szám reciprok értékét és abszolút értékét meghatározni; több műveletből álló és különböző prioritású egyszerűbb számkifejezések értékét kiszámolni ugyanolyan alakban felírt számok esetében, beleértve a zárójelek elhagyását is.
Feladat |
Számold ki mennyi: а) (3/4 - 1/2) · 4 = b) 3,2 · (4,3 + 5,7) =
|
Megoldás |
а) (3/4 - 1/2) · 4 = 1 b) 3,2 · (4,3 + 5,7) = 32
|
Feladat |
|||||||||||||||
Töltsd ki a következő táblázatot:
|
|||||||||||||||
Megoldás |
|||||||||||||||
|
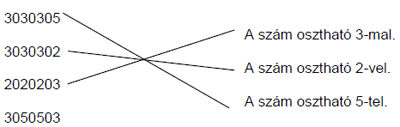
МА.2.1.3. A tanuló tudja a 2, 3, 5, 9 számokra, valamint a 10 hatványaira vonatkozó oszthatósági szabályokat alkalmazni.
Feladat |
||||||||||||||||||||||||
Kösd össze a megadott számokat a megfelelő mondatokkal:
|
||||||||||||||||||||||||
Megoldás |
||||||||||||||||||||||||
|
МА.2.1.4. A tanuló tudja a számokat és számkifejezéseket használni egyszerűbb valós helyzetekben.
Feladat |
25 füzetért 750 dinárt fizettek. Egy füzet 20 dinárral drágább, mint egy ceruza. Hány ceruzát lehetett volna vásárolni ugyanezért a pénzért?
750 dinárért ________ ceruzát lehetett volna vásárolni. |
Megoldás |
750 : 25 = 30 750 dinárért 75 ceruzát lehetett volna vásárolni. |
МА.2.2.1. A tanuló tudja a számolási műveleteket elfogadható szinten elvégezni; tud lineáris egyenleteket és kétismeretlenes lineáris egyenletrendszereket megoldani
Feladat |
|||||||
Karikázd be a helyes válasz előtti betűt.
а) -20 és -10 b) -10 és 10 c) 10 és 20 d) 20 és 30 |
|||||||
Megoldás |
|||||||
c) 10 és 20 |
МА.2.2.2. A tanuló tudja a számolási műveleteket elfogadható szinten elvégezni; tud hatványokkal számolni és tudja mi a négyzetgyök.
Feladat |
||||||||||||
Az igaz állítások esetében karikázd be az IGAZ szót, a hamis állítások esetében pedig a HAMIS szót.
|
||||||||||||
Megoldás |
||||||||||||
|
МА.2.2.3. A tanuló tudja a számolási műveleteket elfogadható szinten elvégezni; tud polinomokat összeadni és kivonni, két binomot összeszorozni és binomot négyzetre emelni.
Feladat |
Az (1/2 • m - n)2 binom négyzete: а) 1/2 • m2 + 2mn + n2 b) 1/4 • m2 - mn + n2 c) 1/2 • m2 - mn + n2 d) 1/4 • m2 - n2 |
Megoldás |
b) 1/4 • m2 - mn + n2 |
МА.2.2.4. A tanuló tudja a számolási műveleteket elfogadható szinten elvégezni; ismerje fel a változók közötti függőséget, ismerje az y=ax függvényt és tudja grafikusan ábrázolni a tulajdonságait; tudja ezeket a tulajdonságokat összekötni az egyenes arányossággal és a fordított arányossággal, valamint tudja az aránypár ismeretlen tagját meghatározni.
Feladat |
||||||||
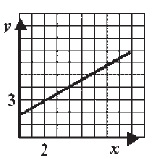
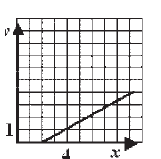
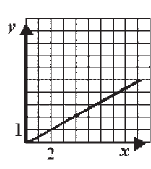
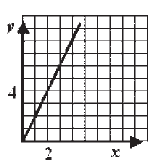
A következő rajzok egyikén grafikusan ábrázoltuk az ólom (х) és a cink (у) közötti függőséget egy olyan ötvözetben, amelyben az ólom és a cink 2:1 arányban fordulnak elő. Karikázd be a grafikon feletti betűt, amely pontosan mutatja be az adott ötvözetben az ólom és a cink közötti függőséget.
|
||||||||
Megoldás |
||||||||
c) |
Feladat |
8 m vászonért 2 400 dinárt kell fizetni. a) Mennyibe kerül ugyanebből a vászonból 12 m? b) Hány métert lehet vásárolni ugyanebből a vászonból 750 dinárért?
а) 12 m vászon _______ dinárba kerül. b) 750 dinárért _________ méter vásznat lehet vásárolni. |
Megoldás |
а) 12 m vászon 3 600 dinárba kerül. b) 750 dinárért 2,5 méter vásznat lehet vásárolni. |
МА. 2.2.5. A tanuló tudja a számolási műveleteket elfogadható szinten elvégezni; tudja az egyenleteket egyszerűbb szöveges feladatokban alkalmazni.
Feladat |
Amikor Péter elköltötte megtakarított pénze egy harmadát mobiltelefonja feltöltésére, akkor összesen 800 dinárja maradt. Mennyi volt Péter megtakarított pénze a vásárlás előtt?
Péter megtakarított pénze a vásárlás előtt _______ dinár volt. |
Megoldás |
Péter megtakarított pénze a vásárlás előtt 1200 dinár volt. |
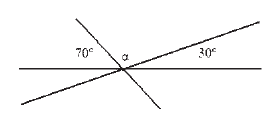
МА.2.3.1. A tanuló tudja a kiegészítő szögeket és pótszögeket, mellékszögeket és csúcsszögeket meghatározni; tudjon számolni velük, ha azok egész fokokban vannak kifejezve.
Feladat |
||
|
||
Megoldás |
||
α = 80° |
МА.2.3.2. A tanuló tudja a háromszög szögeinek és oldalainak viszonyát meghatározni, tudja a háromszög és négyszög belső szögeinek összegét, valamint tudjon feladatokat megoldani a Pitagorasz tétel segítségével.
Feladat |
||
|
||
Megoldás |
||
Ha a vitorla magasága x, akkor x2 = 132 - 52 = 169 - 25 = 144. A vitorla magassága 12 m. A vitorla területe T = 1/2 • 12 • 5 = 30 m2. A vitorla területe 30 m2. |
МА.2.3.3. A tanuló tudja képletek segítségével a kör és körgyűrű kerületét és területét kiszámolni.
Feladat |
A kisebb kör területe 9p cm2. A körgyűrű területe 16p cm2.
A nagyobb kör sugara ____ cm. |
Megoldás |
Tnk = (9p + 16p) cm2 = 25p cm2 A nagyobb kör sugara 5 cm. |
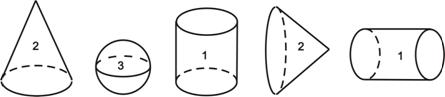
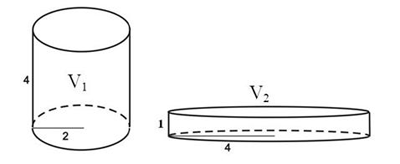
МА.2.3.5. A tanuló tudja a henger, kúp és gömb felszínét és térfogatát kiszámolni, ha a szükséges adatok közvetlenül meg vannak adva a feladatban.
Feladat |
A képen két henger látható, melyeknek térfogata V1 és V2.
Karikázd be a helyes válasz előtti betűt. а) V1 > V2 b) V1 < V2 c) V1 = V2 |
Megoldás |
c) V1 = V2 |
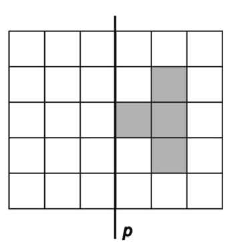
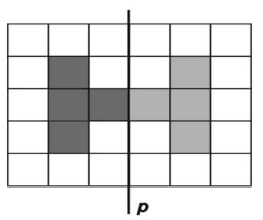
МА.2.3.6. A tanuló ismerje fel a tengelyesen szimmetrikus alakzatokat és tudja az alakzat szimmetriatengelyét meghatározni; tudja alkalmazni az egybevágóságot és tudja azt az alakzat jellegzetes tulajdonságaival összekötni (például a párhuzamosságot a paralelogramma oldalainak egyenlőségével).
Feladat |
Satírozz be négy négyzetet a rajzon úgy, hogy a p egyenesre szimmetrikus alakzatot kapj.
|
Megoldás |
|
МА.2.4.1. A tanuló tudja a hosszúság és tömeg mérése esetében a különböző mértékegységben megadott értékeket összehasonlítani.
Feladat |
|||||||||||||||||||||||||||
A tanárnő felírta a táblára négy tárgy tömegét.
|
|||||||||||||||||||||||||||
Megoldás |
|||||||||||||||||||||||||||
|
Feladat |
Az eladó három, egészben felbontott csirkét árul a boltban, melyeknek tömege 1340 g, 1,35 kg, valamint 1kg 290 g. Rendezd nagyság szerint sorba ezeket a tömegeket, a legnagyobbtól a legkisebbig.
Válasz: ________ > _________ > ________ |
Megoldás |
1,35 kg > 1340 g > 1kg 290 g |
МА.2.4.2. A tanuló tudja az egyik pénznemben megadott összeget a másik pénznembe átalakítani, helyesen használva a megfelelő aránypárokat.
Feladat |
Marcsi az újévi ünnepeket Olaszországban töltötte. Az út és az ott-tartózkodás 200 euróba került. Mekkora összeget fizetett be Marcsi dinárban, ha a befizetés napján 1 euró 105 dinárt ért?
Marcsi _____________ dinárt fizetett be. |
Megoldás |
Marcsi 21000 dinárt fizetett be. |
Feladat |
Ha egy norvég korona 12,50 dinárt ér, egy euró pedig 105 dinárt, akkor mennyit ér 10 euró norvég koronában?
10 euró ______ norvég koronát ér. |
Megoldás |
10 euró 105 • 10 = 1050 dinár. 1050 : 12,5 = 84 10 euró 84 norvég koronát ér. |
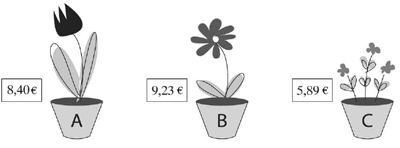
МА.2.4.3. A tanuló tudja egy adott mennyiség közelítőértékét meghatározni.
Feladat |
||||||||
A virágárusnak a legközelebbi egész számra kell kerekítenie a külföldről beszállított virágok árát. Írd be az új árakat.
|
||||||||
Megoldás |
||||||||
|
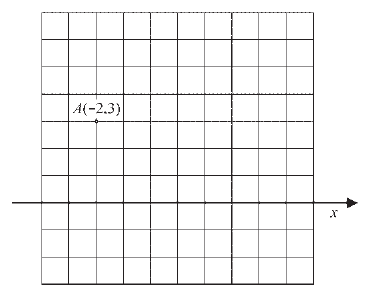
МА.2.5.1. A tanuló képes a koordinátarendszerben való ábrázolásra (tudja a tengelyesen szimmetrikus vagy középpontosan szimmetrikus pont koordinátáit meghatározni, stb.).
Feladat |
Az adott А pont koordinátái alapján rajzold be a derékszögű Descartes-féle koordinátarendszer y-tengelyét.
|
Megoldás |
|
|
МА.2.5.2. A tanuló tudja az egyszerűbb diagramokat és táblázatokat leolvasni és az adatokat egy adott kritérium alapján feldolgozni (például meghatározni egy adathalmaz aritmetikai középértékét; összehasonlítani a minta értékét a középértékkel).
Feladat |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Adott a következő táblázat, amely városok közötti távolságokat mutat be kilométerben kifejezve.
A táblázat alapján egészítsd ki a következő mondatokat úgy, hogy igazak legyenek az állítások. а) A Čačak és Nikšić közötti távolság _______ kilométer. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Megoldás |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) A Čačak és Nikšić közötti távolság 395 kilométer. |
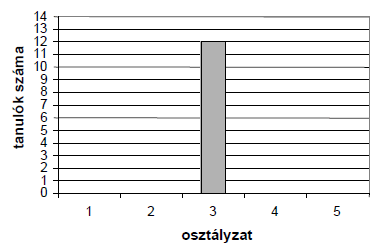
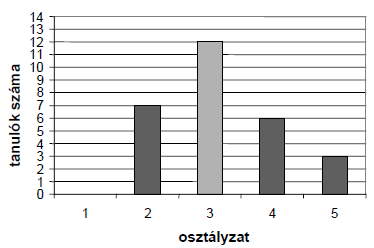
МА.2.5.3. A tanuló tudja az összegyűjtött adatokat feldolgozni, tudja azokat táblázattal vagy grafikusan ábrázolni; tudja a középértéket és a mediánt meghatározni.
Feladat |
||||||||||||||||
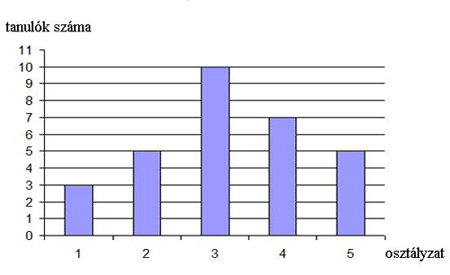
Egy osztály tanulóinak matematikateszten elért eredménye az alábbi diagramon látható.
а) Hasonlóan, mint ahogy elkezdtük, töltsd ki a fenti diagramnak megfelelően a táblázatot:
b) Számold ki a matematikateszten elért átlagosztályzatot. |
||||||||||||||||
Megoldás |
||||||||||||||||
а)
b) A matematikateszten elért átlagosztályzat 3,2. |
||||||||||||||||
МА.3.1.2. A tanuló tudja az oszthatóság fogalmát alkalmazni a problémamegoldásban.
Feladat |
Írj fel három olyan számot, amelyek az ötödik ezresben vannak és a tizeseket jelölő számjegyük 2, de 9-cel is oszthatóak.
Ezek a számok: _______, ________, ________. |
Megoldás |
Bármelyik három szám a következő halmazból {4023, 4122, 4221, 4320, 4329, 4428, 4527, 4626, 4725, 4824, 4923}. |
МА.3.1.3. A tanuló tudja a számokat és számkifejezéseket használni valós helyzetekben.
Feladat |
A virágárus csokrokat készít és árul. Minden csokor 4 rózsát és 3 fehér liliomot tartalmaz. Ha a virágárus minden eladott rózsán 35 dinárt keres, minden eladott fehér liliomon 25 dinárt, minden csokor elkészítésén pedig 60 dinárt, akkor legalább hány csokrot kell elkészítenie, hogy több, mint 1500 dinárt keressen? Írd le a számolás folyamatát.
A virágárusnak legalább _____ csokrot kell eladnia. |
Megoldás |
A kereset egy csokor esetén: 4 • 35 + 3 • 25 + 60 = 140 + 75 + 60 = 275 275 • 5 = 1375, 275 • 6 = 1650 vagy 1500 : 275 = 5,45… A virágárusnak legalább 6 csokrot kell eladnia. |
МА.3.2.2. A tanuló a számolási műveleteket megfelelő biztonsággal tudja elvégezni, alkalmazza és kihangsúlyozza a műveleti azonosságokat; tudja a hatvány és a négyzetgyök tulajdonságait alkalmazni.
Feladat |
Ha tudjuk, hogy 322 = 1024, számold ki mennyi: a) √10,24 = _______________ b) √102400 = _______________ c) √0,1024 = _______________
|
Megoldás |
|
a) √10,24 = 3,2 b) √102400 = 320 v) √0,1024 = 0,32 |
МА.3.2.3. A tanuló a számolási műveleteket megfelelő biztonsággal tudja elvégezni, alkalmazza és kihangsúlyozza a műveleti azonosságokat; tudja a négyzetek különbsége és a binom négyzete képleteket felismerni és alkalmazni; az algebrai kifejezéseket megfelelő biztonsággal átalakítani és azokat a legegyszerűbb alakra hozni.
Feladat |
Karikázd be a helyes válasz előtti betűt. a) а2 − а + 35 b) а2 − а − 37 c) а2 + 35 d) а2 − 37 |
Megoldás |
а) а2 − а + 35 |
Feladat |
Számold ki: а) a 7 és 3 számok négyzeteinek különbségét: __________________________ b) a 7 és 3 számok különbségének négyzetét: __________________________ c) a 7 és 3 számok négyzeteinek összegét: ____________________________ d) a 7 és 3 számok összegének négyzetét: ____________________________ |
Megoldás |
а) 72 - 32 = 49 - 9 = 40 b) (7 − 3)2 = 42 = 16 c) 72 + 32 = 49 + 9 = 58 d) (7 + 3)2 = 102 = 100 |
МА.3.2.4. A tanuló a számolási műveleteket megfelelő biztonsággal tudja elvégezni, alkalmazza és kihangsúlyozza a műveleti azonosságokat; tudja az egyenesen arányos és a fordítottan arányos mennyiségeket megkülönböztetni és tudja ezeket a megfelelő módon felírni; ismerje a lineáris függvényt és tudja a tulajdonságait grafikusan ábrázolni.
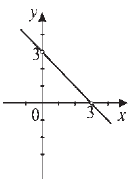
Feladat |
||||||||
Melyik rajz ábrázolja az y = −x + 3 függvény grafikonját?
|
||||||||
Megoldás |
||||||||
|
Feladat |
Egy kilenc emberből álló baráti társaság a medencét négy nap alatt tisztítaná ki. Hány barátjukat kellene még a baráti társaságnak bevonni a munkába, hogy a medencetisztítást három nap alatt elvégezzék? A medencét három nap alatt tisztítanák ki, ha még ____ barátjuk segítene a munkában. |
Megoldás |
9 : x = 3 : 4 vagy x : 9 = 4 : 3 |
МА.3.2.5. A tanuló a számolási műveleteket megfelelő biztonsággal tudja elvégezni, alkalmazza és kihangsúlyozza a műveleti azonosságokat; tudja az egyenleteket és egyenlőtlenségeket, valamint egyenletrendszereket alkalmazni összetettebb szöveges feladatok megoldásában.
Feladat |
||||
A nyaralás ideje alatt Nelli a házban lakó 9 barátjának vagy borítékban írt levelet vagy képeslapot küldött. A képeslapokra 10 dináros, a borítékokra pedig 15 dináros bélyeget kellett vásárolnia. Hány borítékot és hány képeslapot küldött el Nelli, ha bélyegekre összesen 110 dinárt költött el?
Nelli _________ borítékot és _________ képeslapot küldött el. |
||||
Megoldás |
||||
x - borítékok száma
Az egyenletrendszer megoldása x = 5 és y = 4, a megoldási módszertől függetlenül. Nelli 5 borítékot és 4 képeslapot küldött el. |
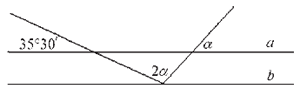
МА.3.3.1. A tanuló tudjon szögekkel számolni beleértve a szögmérték átalakítását is, tudjon következtetéseket levonni a párhuzamos és merőleges egyenesek tulajdonságainak segítségével, beleértve a transzverzálison fekvő szögeket is.
Feladat |
||
Ha a és b párhuzamos egyenesek, határozd meg mekkora az α szög.
|
||
Megoldás |
||
A keresett szög: α =48°10΄ |
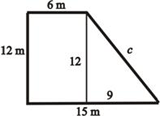
МА.3.3.2. A tanuló tudja a háromszög, négyszög, paralelogramma és trapéz alapvető tulajdonságait alkalmazni, kerületüket és területüket kiszámolni olyan adatok segítségével, amelyek nincsenek közvetlenül megadva a feladat szövegében; tudja ezeket az alakzatokat megszerkeszteni.
Feladat |
||
Hány méter drótra van szükség a képen látható derékszögű trapéz alakú udvar bekerítéséhez? Írd le a számolás folyamatát.
_____ méter drót szükséges. |
||
Megoldás |
||
|
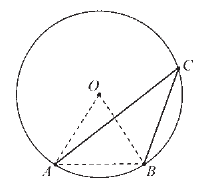
МА.3.3.3. A tanuló tudja a középponti és kerületi szöget meghatározni, a körcikk területét, valamint a körív hosszúságát kiszámolni.
Feladat |
Ha az AB húr hossza egyenlő a kör sugarával, számold ki az ACB szöget.
∠ACB = ______ |
Megoldás |
∠ACB = 30° |
Feladat |
Hányszor kisebb a 30°-os középponti szögű körcikk területe a kör területétől?
____ -szer/szor/ször kisebb. |
Megoldás |
12-szer kisebb. |
МА.3.3.4. A tanuló tudja a hasáb és gúla felszínét és térfogatát kiszámolni, beleértve azokat az eseteket, ahol a szükséges adatok nincsenek közvetlenül megadva.
Feladat |
||
Számold ki a szabályos négyoldalú gúla térfogatát, ha alapéle a = 10 cm, oldallapjának magassága pedig h = 13 cm.
|
||
Megoldás |
||
H2 = h2 - (a/2)2, H2 = 132 - 52, H2 = 169 - 25, H2 = 144, H = 12 cm V = 1/3 • B • H, V = 1/3a2 • H, V = 1/3 • 100 • 12, V = 400 cm3 A gúla térfogata 400 cm3. |
МА.3.3.5. A tanuló tudja a henger, kúp és gömb felszínét és térfogatát kiszámolni, beleértve azokat az eseteket, ahol a szükséges adatok nincsenek közvetlenül megadva
Feladat |
Karikázd be a helyes válasz előtti betűt. A derékszögű háromszöget, melynek befogói а = 9 cm, b = 12 cm, a b befogó körül forgatjuk. A kapott kúp alapterületének és palástfelszínének aránya: а) 1 : 1 b) 3 : 4 c) 3 : 5 d) 4 : 5 |
Megoldás |
c) 3 : 5 |
Feladat |
Mekkora a legnagyobb olyan labdának a felszíne, amelyet belecsomagolhatunk egy 20 cm oldalélű kocka alakú dobozba?
A labda felszíne ____ cm2. |
Megoldás |
A labda felszíne 400p cm2. |
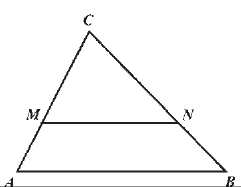
МА.3.3.6. A tanuló tudja a háromszögek egybevágóságát és hasonlóságát alkalmazni, összekötve így a mértani alakzatok különböző tulajdonságait.
Feladat |
||
Az MN szakasz párhuzamos az АВ szakasszal. Ha MN : AB = 2 : 3, mekkora a СМ : MА arány?
|
||
Megoldás |
||
а) 2 : 1 |
Feladat |
||||||||||||
Igaz állítások esetén karikázd be az Igaz szót, а hamis állítások esetében pedig a Hamis szót.
|
||||||||||||
Megoldás |
||||||||||||
|
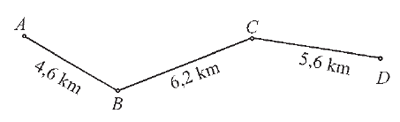
МА.3.4.2. A tanuló tudja a megadott adatokat becsülni és kerekíteni, tudjon az így kapott közelítő-értékekkel tovább számolni; tudjon a hibára becslést adni (például kisebb, mint 1 dinár, 1cm, 1g).
Feladat |
Az А és D helységek közötti távolságot az alábbi térkép szemlélteti.
Dóra úgy adott becslést az А és D helységek közötti távolságra, hogy mindegyik távolságot a legközelebbi egész számú kilométerre kerekítette, majd a kerekített számokat összeadta. Vera összeadta a térképen látható távolságokat, majd a kapott számot a legközelebbi egész kilométerre kerekítette. Karikázd be a helyes válasz előtti betűt. а) Dóra nagyobb számot kapott, mint Vera. b) Dóra és Vera egyenlő számokat kaptak. c) Dóra kisebb számot kapott, mint Vera. |
Megoldás |
а) Dóra nagyobb számot kapott, mint Vera. |
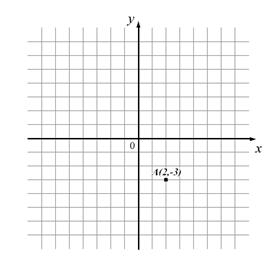
МА.3.5.1. A tanuló tudja összetettebbb feltételeknek eleget tevő pont helyzetét (koordinátáit) meghatározni.
Feladat |
Rajzold be a koordináta-rendszerbe mindazokat a pontokat, amelyek ugyanolyan távolságra vannak az x tengelytől, mint az А pont, az y tengelytől való távolságuk pedig kétszer akkora, mint az A pont y tengelytől való távolsága.
|
Megoldás |
|
МА.3.5.2. A tanuló tudja a diagramokat és táblázatokat értelmezni.
Feladat |
||||||||||||||||||||||||||||||||||||||||||||||||
A táblázatban néhány város közötti távolság adott kilométerekben.
а) Melyik város van Belgrádtól 115 km távolságra? ....................... b) Melyik két város közötti távolság 353 km? ............................................... c) Melyik két város közötti távolság kisebb, mint 50 km? .......................................... d) Hány olyan város van a táblázatban, amely több, mint 200 km távolságra van Belgrádtól? ......... |
||||||||||||||||||||||||||||||||||||||||||||||||
Megoldás |
||||||||||||||||||||||||||||||||||||||||||||||||
а) Kragujevac b) Kraljevo és Szabadka c) Jagodina és Kragujevac d) három |
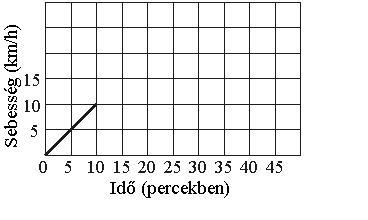
МА.3.5.3. A tanuló képes az adatokat összegyűjteni, belőlük önállóan diagramot vagy táblázatot elkészíteni; tudja a grafikont lerajzolni, amelynek segítségével tudja a mennyiségek közötti függőséget ábrázolni.
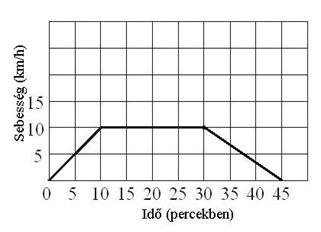
Feladat |
Kata 45 percig kerékpározott. Az első 10 perc után elérte a 10 km/h sebességet. Ezzel a sebességgel további 20 percig folytatta, ezután pedig fokozatosan lassított mindaddig, amíg meg nem állt. Folytasd az elkezdett módon a diagramot, amely leírja Kata kerékpározásának menetét.
|
Megoldás |
|
МА.3.5.4. A tanuló tudja a százalékszámítást alkalmazni összetettebb problémákban.
Feladat |
A könyv árát először felemelték 10%-kal, majd leengedték 10%-kal, így most 198 dinárba kerül. Mennyi volt a könyv ára a drágulás előtt? Karikázd be a helyes válasz előtti betűt. а) 198 dinár b) 200 dinár c) 202 dinár d) 196,02 dinár |
Megoldás |
b) 200 dinár |
Követelményrendszer a kötelező oktatás végére matematikából, ahol a számonkérés ismeretlen feladatokon keresztül történik
МА.2.3.4. A tanuló ismerje a: hasáb és gúla fogalmát; tudja felszínüket és térfogatukat kiszámolni, ha a szükséges adatok közvetlenül meg vannak adva a feladatban.
Feladat |
Egy szabályos háromoldalú egyenlőélű gúla alapéle 8 cm. Mekkor a gúla felszíne?
A gúla felszíne ___________ cm2 |
Megoldás |
TA = a2/4 • √3 = 16√3 cm2 F = 4 • TA = a2√3 = 64√3 cm2 vagy F = 4 • (a2/4)√3 = a2√3 = 64√3 cm2 A gúla felszíne 64√3 cm2. |
МА.2.5.4. A tanuló tudja a százalékszámítást alkalmazni az egyszerűbb valós problémákban (például, adott termék árát adott százalékkal megváltoztatni).
Feladat |
Gabriella fagylaltot árul. Minden eladott 60 dináros fagylalton, ő maga 6 dinárt keres. Mennyi Gabriella keresete egy fagylalton százalékban kifejezve? а) 6 % b) 1 % c) 54 % d) 10 % |
Megoldás |
d) 10 % |
МА.3.1.1. A tanuló tudja az összetettebb számkifejezések értékét meghatározni.
Feladat |
Számold ki az А és В számkifejezések szorzatát, ha A = 1 + 3 : (6/5) - 2/5 • 5/4 és B = 8/3 - 7/3 • 6/7.
А = _______ , B = ______ , szorzatuk A · B = _______ |
Megoldás |
А = 3, B = 2/3, szorzatuk A • B = 2 |
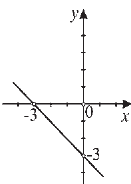
МА.3.2.1. A tanuló a számolási műveleteket megfelelő biztonsággal tudja elvégezni, alkalmazza és kihangsúlyozza a műveleti azonosságokat; tudja a lineáris egyenleteket és egyenlőtlenségeket, valamint a kétismeretlenes lineáris egyenletrendszereket felállítani és megoldani.
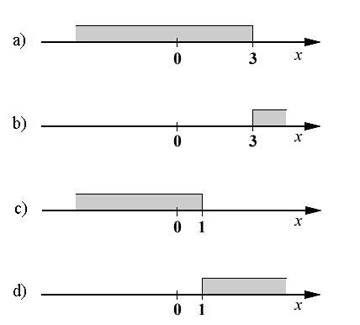
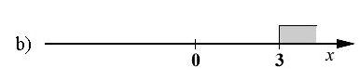
Feladat |
A számegyenesen ábrázolt halmazok közül melyik a megoldáshalmaza a 4 - (6 - 2x)/3 > 4 egyenlőtlenségnek? Karikázd be a helyes válasz előtti betűt.
|
Megoldás |
|
МА.3.4.1. A tanuló tudja a mértékegységeket szükség szerint átváltani, képes velük számolni.
Feladat |
A film 22 óra 10 perckor fejeződött be. Mikor kezdődött a film, ha 115 percig tartott? Karikázd be a helyes válasz előtti betűt. а) 20 óra és 55 perc b) 20 óra és 45 perc c) 20 óra és 15 perc d) 20 óra és 5 perc |
Megoldás |
c) 20 óra 15 perc |









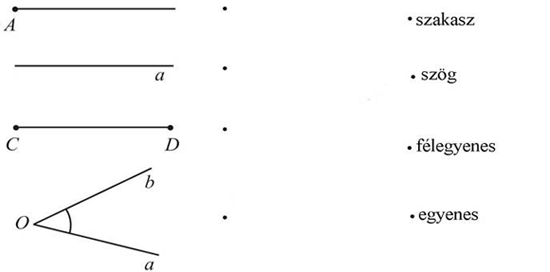
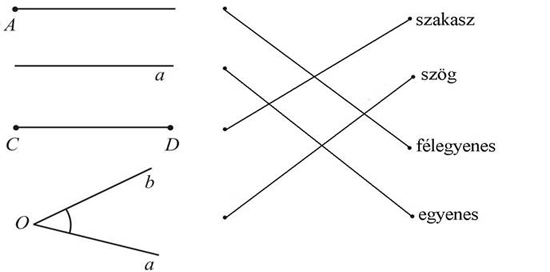
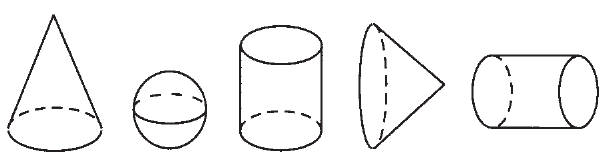




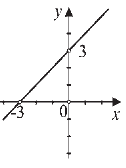
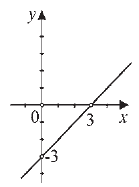



 .
.