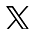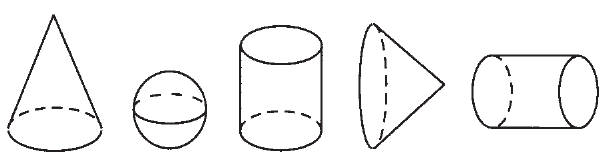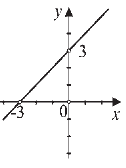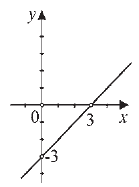PRAVILNIK O PROGRAMU ZAVRŠNOG ISPITA U OSNOVNOM OBRAZOVANJU I VASPITANJU("Sl. glasnik RS - Prosvetni glasnik", br. 1/2011, 1/2012, 1/2014, 12/2014, 2/2018, 3/2021, 14/2022, 4/2023 i 5/2023 - ispr.) |
U oblasti PISANO IZRAŽAVANJE učenik/učenica:
SJ.3.2.1. organizuje tekst u logične i pravilno raspoređene pasuse; određuje prikladan naslov tekstu i podnaslove delovima teksta
Zadatak |
Napiši referat o motivu slobode u poeziji Đure Jakšića, pozivajući se na pesmu Otadžbina. Pre nego što počneš da pišeš referat, sastavi plan za pisanje, osmisli i rasporedi osnovne celine (tri do četiri) i daj naslov referatu. |
Otadžbina I ovaj kamen zemlje Srbije, Vekova tavnih to su tragovi, I samo dotle, do tog kamena, |
|
|||||||||
Rešenje |
|||||||||
Ocenjuje se u kojoj je meri odgovoreno na temu, koliko je naslov prikladan, da li su delovi organizovani logičnim redosledom. |
SJ.3.2.2. sastavlja argumentativni tekst
Zadatak |
Roditelji su ti saopštili da razmišljaju o preseljenju u veći grad. Voleli bi da čuju i tvoje mišljenje. Tvoj zadatak je da dobro razmisliš o ovom predlogu, odlučiš se da li si za preseljenje ili protiv njega, smisliš moguće razloge i obrazloženja za svoju odluku i sve to napišeš. Za ovaj zadatak imaš ukupno 90 minuta. Za to vreme treba da odlučiš koji ćeš stav zastupati (za preseljenje ili protiv njega), da smisliš argumente i obrazloženja kojima ćeš braniti svoj stav, zatim da napišeš rad, ponovo ga pročitaš, proveriš ima li grešaka i ispraviš sve greške koje uočiš. Ne zaboravi da svom radu daš i naslov. Tvoj rad će se ocenjivati na osnovu toga: Molimo te da pišeš čitko. Srećan rad!
|
Rešenje |
Ocenjuje se koliko je tekst jasan, celovit i koherentan, koliko jasno je iznet i obrazložen stav o preseljenju, koliko su uzeti u obzir i argumenti koji se ne slažu sa tim stavom i koliko se poštuju pravopisna pravila. |
SJ.3.2.3. piše prikaz (knjige, filma, pozorišne predstave i sl.), reportažu i raspravu
Zadatak |
||||||||
Napiši raspravu o sledećoj temi: ULOGA MODE U SAVREMENOM SVETU. Ljudi imaju različita mišljenja o tome koliko je važna moda u savremenom životu. Rasprava koju ćeš napisati treba da počne navođenjem različitih mišljenja o toj temi, da se nastavi iznošenjem argumenata i završi zaključkom. Takođe, imaj na umu da se moda ne odnosi samo na odevanje već i na mnoge druge pojave. ULOGA MODE U SAVREMENOM SVETU
|
||||||||
Rešenje |
||||||||
Ocenjuje se koliko je rasprava jasna, celovita i koherentna, koliko su jasno i precizno navedeni ubedljivi argumenti i da li zaključak sledi iz njih. |
SJ.3.2.4. piše rezime dužeg i/ili složenijeg teksta
Zadatak |
||||||
Pročitaj sledeći tekst, a potom napiši sažetak teksta u četiri do šest rečenica. Razmisli o tome šta je cilj autora teksta i koje su najvažnije informacije iznete u tekstu. Škola Svi znamo šta je to škola i šta se u školi radi. Tu se uči, stiče znanje potrebno za život, rešavaju teški i ozbiljni zadaci, savladavaju razne nauke i veštine: od nauke o jeziku do fizičke kulture. To je, dakle, veoma važna i ozbiljna ustanova. Očekivali bismo stoga da tako važna i ozbiljna ustanova ima i važno, ozbiljno, pa čak i strogo ime. Ali - ništa od svega toga! Iznenadićete se kad saznate šta, u stvari, znači reč škola, ili, bolje reći, šta je nekada značila.
Sažetak
|
||||||
Rešenje |
||||||
Ocenjuje se da li sažetak sadrži najvažnije informacije (o poreklu reči škola, šta je škola nekad bila). U njemu ne sme da bude manje važnih informacija i detalja. |
SJ.3.2.5. zna i dosledno primenjuje pravopisnu normu
Zadatak |
U sledećim rečenicama upiši zapetu tamo gde je potrebno. a) Jednom rečju s mojom sestrom nikada ne može biti dosadno. b) Neki domaćin dobar čovek lepo ga primi. |
Rešenje |
Jednom rečju, s mojom sestrom nikada ne može biti dosadno. |
3. GRAMATIKA, LEKSIKA, NARODNI I KNJIŽEVNI JEZIK
U podoblasti GRAMATIKA učenik/učenica:
SJ.3.3.1. deli reč na slogove u složenijim slučajevima
Zadatak |
|||||||||
Podeli uspravnim crtama sledeće reči na slogove:
|
|||||||||
Rešenje |
|||||||||
|
|||||||||
SJ.3.3.2. poznaje glasovne promene (ume da ih prepozna, objasni i imenuje)
Zadatak |
||||||||||||
Napiši koja se glasovna promena ne vrši u oblicima datih reči, iako postoje uslovi za njeno vršenje:
|
||||||||||||
Rešenje |
||||||||||||
a) sibilarizacija |
Zadatak |
|||||||||||||||
|
|||||||||||||||
Rešenje |
|||||||||||||||
a) pečem, palatalizacija |
|||||||||||||||
SJ.3.3.3. zna i u svom govoru primenjuje akcenatsku normu
Zadatak |
||||||||||||
Pročitaj stihove iz pesme Miroslava Antića Plava zvezda. Stihove smo obeležili brojevima. 1. Mora biti takve zvezde. Zaokruži u tabeli T, ako je tvrdnja tačna, a ako je netačna, zaokruži N.
|
||||||||||||
Rešenje |
||||||||||||
T |
SJ.3.3.5. poznaje i imenuje podvrste sintaksičkih jedinica (vrste sintagmi, nezavisnih i zavisnih predikatskih rečenica)
Zadatak |
Odredi vrstu podvučene sintagme u sledećoj rečenici: Odmah posle doručka otišao sam u strmu baštu iznad kuće. Podvučena sintagma u rečenici po vrsti je _______________.
|
Rešenje |
imenička |
Zadatak |
|||||||||
Odredi vrstu podvučenih zavisnih rečenica:
|
|||||||||
Rešenje |
|||||||||
a) uzročna |
SJ.3.3.6. poznaje glavna značenja padeža i glavna značenja glagolskih oblika (ume da ih objasni i zna terminologiju u vezi s njima)
Zadatak |
Zaokruži slovo ispred rečenice u kojoj glagolski prilog sadašnji ima uzročno značenje. |
a) Tako idući niz vodu, dečaci naiđu na svoju vodenicu. b) Milan i Stojan se vrate kući, čudeći se šta će to biti. v) Patuljak nije isprva hteo da ide u krađu, plašeći se kazne. g) Slušajući radio, posmatrala je ptice u svom dvorištu. |
Rešenje |
v) Patuljak nije isprva hteo da ide u krađu, plašeći se kazne. |
U podoblasti LEKSIKA učenik/učenica:
SJ.3.3.7. ume da odredi značenja nepoznatih reči i izraza na osnovu njihovog sastava, konteksta u kome su upotrebljeni, ili na osnovu njihovog porekla
Zadatak |
Pažljivo pročitaj sledeći tekst i reši zadatak: Muzika Indije u starom veku Muzika stare Indije ima poseban oblik. Indijski napev karakteriše lestvica širokog opsega, kao i slobodniji ritmički i formalni tok. Stari Indusi pravili su veliku razliku između duhovne i svetovne muzike. Duhovni napevi bili su zasnovani na tekstovima verskih knjiga (Veda) i bili su mirni, spori i dostojanstveni. U osnovi svetovne muzike bili su stalni melodijski obrasci, koje je umetnik varirao i obogaćivao ornamentiranjem. Ovi napevi uvek su se pevali u utvrđeno vreme i u različitim prilikama. Podvučeni skup reči označava: a) jednoličnu muziku: |
Rešenje |
v) narodnu muziku |
SJ.3.3.8. zna značenja reči i frazeologizama u naučnopopularnim tekstovima, namenjenim mladima, i pravilno ih upotrebljava
Zadatak |
||
Među ponuđenim rečima zaokruži onu čije značenje odgovara izostavljenoj reči u rečenici: aktivna, formalna, toksična, sekundarna. Naučnici ispituju u laboratorijama hemijski sastav široko rasprostranjene biljke - ptičje mleko, jer su uočili da sadrži supstance koje uspešno suzbijaju umnožavanje obolelih ćelija, ali smatraju da je suviše _______________ i još uvek je ne preporučuju za upotrebu. |
||
Rešenje |
||
|
U oblasti KNJIŽEVNOST učenik/učenica:
SJ.3.4.1. navodi naslov dela, autora, rod i vrstu na osnovu odlomaka, likova, karakterističnih tema i motiva
Zadatak |
||||||||
Pročitaj sledeći tekst. Sterija u svom delu prikazuje ličnost koja pokušava da stekne uglađene i fine manire. Ona to čini tako što koristi izraze na francuskom i nemačkom, ali ne samo da ne zna dobro te jezike nego ni srpski ne govori pravilno. Njen brat i ćerka pokušavaju da je urazume. Na linijama upiši odgovore na sledeća pitanja:
|
||||||||
Rešenje |
||||||||
Pokondirena tikva |
Zadatak |
||||||
U jednom romanu iz tvoje lektire prikazana je svađa popadija i tuča popova zbog zeta. Data je slika života u vojvođanskom selu. Roman obiluje anegdotskim situacijama. O kom romanu je reč u navedenom tekstu? Ko je napisao taj roman?
|
||||||
Rešenje |
||||||
Pop Ćira i pop Spira Stevan Sremac |
SJ.3.4.2. izdvaja osnovne odlike književnih rodova i vrsta u konkretnom tekstu
Zadatak |
Pročitaj stihove iz pesme Proleće Miroslava Antića. Koje odlike lirske pesme prepoznaješ u tim stihovima? Sunce se, eno, Bila je zima. Odlike: |
Rešenje |
|
SJ.3.4.3. razlikuje autora dela od lirskog subjekta i pripovedača u delu
Zadatak |
Odredi ko je lirski subjekt u stihovima iz pesme Marija Dušana Radovića: Ja sam bila nežni cvetak, Lirski subjekt je: Zaokruži slova ispred tačnih odgovora. |
Rešenje |
|
SJ.3.4.4. pronalazi i imenuje stilske figure; određuje funkciju stilskih figura u tekstu
Zadatak |
Napiši nazive stilskih figura iz podvučenog stiha: Ljubičaste gore, granitne, do svoda. Nazivi stilskih figura: |
Rešenje |
onomatopeja |
Zadatak |
Pročitaj stihove iz pesme Ženidba Milića barjaktara. Oj, punice, đevojačka majko, "Mio zete, Milić barjaktare, Naziv stilske figure je ____________________. |
Rešenje |
slovenska antiteza |
SJ.3.4.5. određuje i imenuje vrstu stiha i strofe
Zadatak |
Pročitaj stihove iz pesme Veče Vojislava Ilića. Na osnovu broja stihova u strofi, navedi naziv vrste strofe. Rumene pruge već šaraju daleki zapad, Sve grli mir i san. Pokašto zaurla samo Naziv vrste strofe: ____________________ |
Rešenje |
katren |
SJ.3.4.7. izražava svoj stav o konkretnom delu i argumentovano ga obrazlaže
Zadatak |
|||
Pročitaj Dučićevu pesmu Podne, a zatim odgovori na pitanja. Nad ostrvom punim čempresa i bora, Ljubičaste gore, granitne, do svoda. Prah sunčani trepti nad ispranim peskom, Sve je tako tiho. I u mojoj duši Nemo stoje u njoj srebrnaste, rodne Koja je strofa u ovoj pesmi ostavila najveći utisak na tebe? Obrazloži odgovor.
|
|||
Rešenje |
|||
Prihvatljivi su odgovori u kojima učenik na različite načine obrazlaže svoj utisak, pozivajući se na pesmu. Na primer, ukoliko učenik izabere prvu strofu, očekuje se da će pisati o tome kako je pesnik slikama čempresa, bora, jačine sunčevih zraka podstakao čulni doživljaj u njemu kao čitaocu. |
SJ.3.4.8. povezuje književnoumetničke tekstove s drugim tekstovima koji se obrađuju u nastavi
Zadatak |
||||||||
Pročitaj odlomak iz eseja Peđe Milosavljevića Potera za pejzažima i komentar o ovom umetniku. 1. Evo nas, najzad, na kraju sveta. Sve prestaje, jer se i samo nebo survalo pod noge, u plavu, ogromnu provaliju, bez kraja i početka. Jesu li kiparisi ova zelena vretena kojim se kite svi preostali bregovi? A plave šume, možda masline? Na suprotnoj strani pojavljuje se novi, uzani zaliv, dubok i plav. Na njegovoj glatkoj površini, kao ljuske, leže beli čamci u pratnji belih senki na samom dnu. Oko voza kruže galebovi. Plavo beskrajno more kao da je pod samim točkovima. 2. Slikar i književnik, Peđa Milosavljević ispoljava svoj slikarski dar i u esejima i zapisama. To je vidljivo i u ovom tekstu u načinu na koji pisac oblikuje pejzaže. Živopisne boje i izbor pejzaža podsećaju na slikare. Voleo je da slika pejzaže, stare kuće, manastire, prirodu, cveće i drugo. Poznate su mu knjige eseja i zapisa Između trube i tišine i Beograd, grad na moru. Uoči sličnosti i razlike između ova dva teksta. Ukoliko je tvrdnja tačna, upiši T, ako nije, upiši N.
|
||||||||
Rešenje |
||||||||
|
Obrazovni standardi za kraj obaveznog obrazovanja
za srpski jezik koji će biti ispitivani nepoznatim zadacima
SJ.2.1.4. razlikuje sve delove teksta i knjige, uključujući indeks, pojmovnik i bibliografiju i ume njima da se koristi
Zadatak |
Pred tobom je jedna strana indeksa iz Gramatike srpskog jezika za osnovnu školu. Pažljivo je pogledaj i odgovori na postavljeno pitanje.
Šta označava broj iza popisa u indeksu? Zaokruži slovo ispred tačnog odgovora: a) broj paragrafa u kome se govori o tom pojmu; |
Rešenje |
b) broj strane na kojoj se govori o tom pojmu |
SJ.2.1.6. razlikuje činjenicu od komentara, objektivnost od pristrasnosti i propagande na jednostavnim primerima
Zadatak |
Pročitaj odlomak iz dela Umetnost i njena istorija. U tekstu autor govori o jednom starogrčkom reljefu i daje svoj komentar o tom reljefu. Podvuci rečenicu u kojoj je iskazan komentar. "Na ovom reljefu Atlas je prikazan kako se vraća sa zlatnim jabukama do Herakla, koji stoji pod svojim golemim teretom. Atina mu je podmetnula jastuče na ramena. U desnoj ruci nekad je držala metalno koplje. Čitava je priča ispričana s divnom jednostavnošću i jasnoćom. Atina je okrenuta prema nama i samo joj je glava okrenuta u stranu ka Heraklu." |
Rešenje |
Čitava je priča ispričana s divnom jednostavnošću i jasnoćom. |
SJ.3.1.3. izdvaja iz teksta argumente u prilog nekoj tezi (stavu) ili argumente protiv nje; izvodi zaključke zasnovane na složenijem tekstu
Zadatak |
||||||
Pažljivo pročitaj sledeći tekst o novčanicama u Srbiji Sredinom 19. veka Srbija je još vazalna kneževina, deo Turskog carstva, zemlja koja nema pravo na štampanje sopstvenog novca. U Kneževini Srbiji u to doba koriste se 42 monete susednih država, među kojima je najzastupljeniji turski novac. Sa željom za državnom samostalnošću i nezavisnošću od Turske, u srpskom narodu javlja se i potreba za sopstvenim novcem. Izdavanjem prvih bakarnih kovanica knez Mihailo Obrenović započeo je ostvarenje ovog sna, a 1876. godine knez Milan je naručio prve otiske papirnog novca. "Državne novčanice", kako piše na licu novčanice, "izdaju se na osnovu zakonodavne odluke od 19. januara 1876". Pored ove objave, stoji i upozorenje da svako "ko pravi lažne novčanice i ko se njima služi, kazniće se po paragrafu 145. i 146. krivičnog zakona". Državna štamparija u Beogradu štampala je novčanice od jednog, pet, deset, pedeset i sto dinara, i to po 1500 primeraka od svake vrednosti. Ali, u julu 1875. godine, hercegovački ustanak preokrenuo je stanje u zemlji. Srbija se pripremala za rat protiv Turske iako su se evropske sile protivile. Zbog toga u Srbiju nikada nije stigao inostrani zajam od 24 miliona dinara koji je trebalo da služi kao zlatna podloga prilikom štampanja srpskog novca. Tadašnje vlasti zaključile su da nisu stvoreni uslovi za puštanje novca u promet i odlučile da čekaju srećnija vremena. Prva novčanica koja je izdata u Srbiji i bila u upotrebi nosi datum osnivanja Privilegovane narodne banke Kraljevine Srbije - 2. jul 1884. godine. Vrednost novčanice bila je 100 dinara, plativih u zlatu, i njena pojava izazvala je oduševljenje u narodu. Građani su nosili u banku protivvrednost u zlatu da bi je otkupili, što pokazuje koliko je poverenje uživala kod ljudi, Novac će u Srbiji dugo ostati stabilan, uprkos ratovima koji su se vodili na njenom tlu. Balkanski ratovi, aneksiona kriza i Prvi svetski rat nisu naudili dinaru. Zasluga za ovaj "podvig" pripada Đorđu Vajfertu, guverneru Narodne banke u ratno doba. On je u toku rata redovno isplaćivao dugove Nemačkoj i tako uspeo da očuva ugled srpskog dinara. Kao simbol sigurnosti dinara i privatnog vlasništva, lik Đorđa Vajferta danas se nalazi na novčanici od hiljadu dinara. Vajfert je 1917. godine u Marselju (gde je bila izmeštena Narodna banka Srbije) štampao novčanicu od pet dinara plativih u srebru. Prednja strana novčanice s likom Miloša Obilića ispisana je na srpskom jeziku. a zadnja na francuskom. U zaglavlju novčanice velikim slovima piše "BOG ČUVA SRBIJU", a banka ponovo podseća da se "falsifikovanje banknota kažnjava robijom". Iz teksta saznajemo da je srpska vlada u jednom istorijskom trenutku zaustavila štampanje pripremljenih novčanica. Navedi argumente iz teksta koji objašnjavaju taj potez srpske vlade.
|
||||||
Rešenje |
||||||
Kao tačan odgovor priznaju se argumenti navedeni u tekstu: izbio je hercegovački ustanak, Srbija se pripremala za rat, iako su se evropske sile protivile i zbog toga Srbija nije dobila zajam koji je trebalo da služi kao zlatna podloga. |
SJ.3.3.4. poznaje podvrste reči; koristi terminologiju u vezi sa vrstama i podvrstama reči i njihovim gramatičkim kategorijama
Zadatak |
||||||
Napiši nazive podvučenih glagolskih oblika u sledećoj rečenici: Vrativši se kući, izvalio se obučen preko postelje i istog trena potonuo je u san.
|
||||||
Rešenje |
||||||
|
Zadatak |
||||||||||||||||||||||||||||||||||||
Upiši u tabelu osnovni oblik navedene reči i naziv vrste kojoj ta reč pripada. Dva primera su urađena. Međutim, nisam imao mnogo razloga da budem toliko ponosan na te pantalone koje su mi navukli. To su bile pantalone moga starijega brata i na njima je bila ispisana cela njegova kratka, ali burna biografija.
|
||||||||||||||||||||||||||||||||||||
Rešenje |
||||||||||||||||||||||||||||||||||||
međutim - međutim - REČCA |
Zadatak |
||||||||||||||||||
Popuni prazna polja u tabeli, kao što je započeto
|
||||||||||||||||||
Rešenje |
||||||||||||||||||
|
SJ.3.4.6. tumači različite elemente književnoumetničkog dela pozivajući se na samo delo
Zadatak |
Pročitaj odlomak iz Autobiografije Branislava Nušića. Dok čitaš, razmišljaj o kakvoj se poeziji pripoveda u tekstu. Napisao sam svega dve pesme u životu i sa obema sam toliko stradao da sam se zarekao čak i da ne čitam više stihove, a kamoli još i da ih pišem. O, koliko me je puta gonilo i golicalo nešto u duši, koliko puta me je držala inspiracija, koliko puta mamila kakva prilika, ali sam se uvek junački uzdržao. O kakvoj poeziji je reč u ovom tekstu? a) koja je teško razumljiva; b) bez iskrenih osećanja; v) priznatih pesnika; g) bez rime. |
Rešenje |
b) bez iskrenih osećanja |
Obrazovni standardi za kraj obaveznog obrazovanja za
matematiku sa primerima zadataka
MA.1.1.1. Učenik ume da pročita i zapiše različite vrste brojeva (prirodne, cele, racionalne)
Zadatak |
||||||||||||||||||||||||||||
Poveži linijama jednake brojeve kao što je započeto:
|
||||||||||||||||||||||||||||
Rešenje |
||||||||||||||||||||||||||||
Sve tačno povezano. 3/10 povezano sa tri desetine; 3/2 povezano sa tri polovine; 2/5 povezano sa dve petine |
MA.1.1.2. Učenik ume da prevede decimalni zapis broja u razlomak i obratno.
Zadatak |
Koji od ponuđenih brojeva je jednak broju 0,3? |
Rešenje |
b) 3/10 |
MA.1.1.3. Učenik ume da uporedi po veličini brojeve istog zapisa, pomažući se slikom kad je to potrebno.
Zadatak |
|||||||||
Dati su brojevi |
|||||||||
|
|||||||||
|
|||||||||
Rešenje |
|||||||||
|
MA.1.1.4. Učenik ume da izvrši jednu osnovnu računsku operaciju sa brojevima istog zapisa, pomažući se slikom kada je to potrebno (u slučaju sabiranja i oduzimanja razlomaka samo sa istim imeniocem); računa na primer 1/5 od n, gde je n dati prirodan broj.
Zadatak |
Izračunaj i napiši odgovarajući rezultat. |
Rešenje |
a) -3; b) -8; v) -12; g) -4 |
MA.1.1.5. Učenik ume da deli sa ostatkom jednocifrenim brojem i zna kada je jedan broj deljiv drugim.
Zadatak |
||||||||||||||||||
Popuni sledeću tabelu kao što je započeto.
|
||||||||||||||||||
Rešenje |
||||||||||||||||||
Ostatak pri deljenju 123 sa 2 je 1; ostatak pri deljenju 237 sa 3 je 0 i ostatak pri deljenju 128 sa 5 je 3. |
MA.1.1.6. Učenik ume da koristi cele brojeve i jednostavne izraze sa njima pomažući se vizuelnim predstavama.
Zadatak |
Danas je Jovanin rođendan i ona će za tri godine napuniti 18 godina. Koliko Jovana danas ima godina? Zaokruži slovo ispred tačnog odgovora. a) 12 b) 15 v) 18 g) 21 |
Rešenje |
b) 15 |
MA.1.2.1. Učenik vrši formalne operacije koje su reducirane i zavise od interpretacije; ume da reši linearne jednačine u kojima se nepoznata pojavljuje samo u jednom članu.
Zadatak |
Koji broj je rešenje jednačine x/2+ 2 = 8? Zaokruži slovo ispred tačnog odgovora. a) 5 b) 6 v) 12 g) 20 |
Rešenje |
v) 12 |
MA.1.2.2. Učenik vrši formalne operacije koje su reducirane i zavise od interpretacije; ume da izračuna stepen datog broja, zna osnovne operacije sa stepenima.
Zadatak |
Zaokruži slovo ispred tačnog odgovora. Proizvod 210· 22 jednak je: a) 25 b) 28 v) 212 g) 220 |
Rešenje |
v) 212 |
Zadatak |
Zaokruži slovo ispred tačnog odgovora. Vrednost stepena 0,32 je: a) 0,06 b) 0,6 v) 0,09 g) 0,9 |
Rešenje |
v) 0,09 |
MA.1.2.3. Učenik vrši formalne operacije koje su reducirane i zavise od interpretacije; ume da sabira, oduzima i množi monome.
Zadatak |
Sredi sledeće izraze: a) 5a3 + 7a3 = b) 9x2 - 4x2 = v) 2b · 3b2 = |
Rešenje |
a) 12a3 b) 5x2 v) 6b3 |
MA. 1.2.4. Učenik vrši formalne operacije koje su reducirane i zavise od interpretacije; ume da odredi vrednost funkcije date tablicom ili formulom.
Zadatak |
|||||||||||
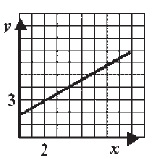
Funkcija je data formulom y = 2x +1. Izračunaj odgovarajuće vrednosti promenljivih x i y i popuni tabelu.
|
|||||||||||
Rešenje |
|||||||||||
Za x = 0 y = 1; za y = 5 x = 2; za x = 4 y = 9. |
MA.1.3.1. Učenik vlada pojmovima: duž, poluprava, prava, ravan i ugao (uočava njihove modele u realnim situacijama i ume da ih nacrta koristeći pribor; razlikuje neke vrste uglova i paralelne i normalne prave).
Zadatak |
Poveži sliku sa nazivom figure koju ta slika predstavlja.
|
Rešenje |
Sve tačno povezano. Slika poluprave povezana sa poluprava; slika prave povezana sa prava; slika duži povezana sa duž i slika ugla povezana sa ugao. |
MA.1.3.2. Učenik vlada pojmovima: trougao, četvorougao, kvadrat i pravougaonik (uočava njihove modele u realnim situacijama i ume da ih nacrta koristeći pribor; učenik razlikuje osnovne vrste trouglova, zna osnovne elemente trougla i ume da izračuna obim i površinu trougla, kvadrata i pravougaonika na osnovu elemenata koji neposredno figurišu u datom zadatku; ume da izračuna nepoznatu stranicu pravouglog trougla primenjujući Pitagorinu teoremu.
Zadatak |
Koliku površinu poda pokriva tepih oblika pravougaonika dužine 3,5 m i širine 2 m? Zaokruži slovo ispred tačnog odgovora. a) 11 m2 b) 7 m2 v) 5,5 m2 g) 3,5 m |
Rešenje |
b) 7 m2 |
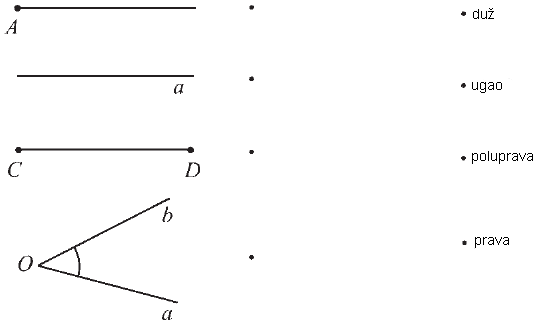
Zadatak |
||
|
||
Rešenje |
||
c = 10 cm |
MA.1.3.3. Učenik vlada pojmovima: krug, kružna linija (izdvaja njihove osnovne elemente, uočava njihove modele u realnim situacijama i ume da ih nacrta koristeći pribor; ume da izračuna obim i površinu kruga datog poluprečnika).
Zadatak |
Koliki je obim kruga čiji je poluprečnik 7 cm? Zaokruži slovo ispred tačnog odgovora. a) 14 cm b) 49 cm v) 14π cm g) 49π cm |
Rešenje |
v) 14π cm |
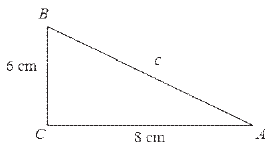
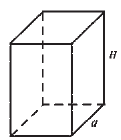
MA. 1.3.4. Učenik vlada pojmovima: kocka i kvadar (uočava njihove modele u realnim situacijama, zna njihove osnovne elemente i računa njihovu površinu i zapreminu).
Zadatak |
||
|
||
Rešenje |
||
Površina prizme je 312 cm2. |
MA.1.3.5. Učenik vlada pojmovima: kupa, valjak i lopta (uočava njihove modele u realnim situacijama, zna njihove osnovne elemente).
Zadatak |
Na svaku sliku koja predstavlja valjak upiši broj 1, na svaku sliku koja predstavlja kupu upiši broj 2 i na svaku sliku koja predstavlja loptu upiši broj 3.
|
Rešenje |
Redom u tela upisani brojevi 2, 3, 1, 2, 1. |
MA.1.3.6. Učenik intuitivno shvata pojam podudarnih figura (kretanjem do poklapanja).
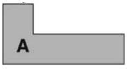
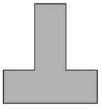
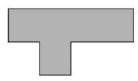
Zadatak |
||||||||
Koja figura na slici je podudarna sa figurom A?
|
||||||||
Zaokruži slovo iznad tačnog odgovora.
|
||||||||
Rešenje |
||||||||
v) |
Zadatak |
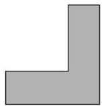
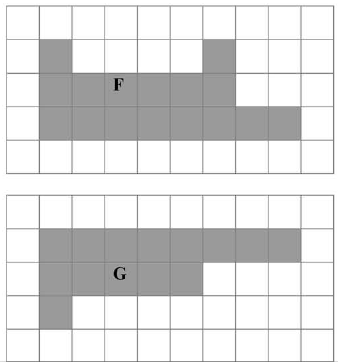
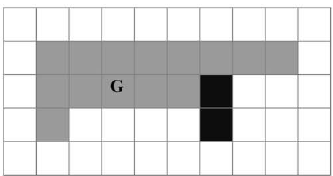
Data je figura F. Oboj šta je potrebno da figura G bude podudarna sa figurom F.
|
Rešenje |
|
MA.1.4.1. Učenik ume da koristi odgovarajuće jedinice za merenje dužine, površine, zapremine, mase, vremena i uglova.
Zadatak |
|||||||||||||||
Prazno polje u tabeli popuni odgovarajućom mernom jedinicom
|
|||||||||||||||
Rešenje |
|||||||||||||||
|
MA.1.4.2. Učenik ume da pretvori veće jedinice dužine, mase i vremena u manje.
Zadatak |
Koji vremenski period je najduži? Zaokruži slovo ispred tačnog odgovora. a) tri meseca b) 100 dana v) 10 nedelja g) četvrtina godine |
Rešenje |
b) 100 dana |
MA.1.4.3. Učenik ume da koristi različite apoene novca.
Zadatak |
Ako razmeniš 3 novčanice od 200 dinara novčanicama od 50 dinara, koliko ćeš novčanica dobiti?
Dobiću _____ novčanica od 50 dinara. |
Rešenje |
Dobiću 12 novčanica od 50 dinara. |
MA.1.4.4. Učenik ume da pri merenju odabere odgovarajuću mernu jedinicu zaokrugljuje veličine iskazane datom merom.
Zadatak |
||||||||||||||||||
U prazno polje upiši odgovarajuću mernu jedinicu: km, cm, l, kg ili g. |
||||||||||||||||||
|
||||||||||||||||||
Rešenje |
||||||||||||||||||
|
MA.1.5.1. Učenik ume da izražava položaj objekata svrstavajući ih u vrste i kolone; odredi položaj tačke u prvom kvadrantu koordinatnog sistema ako su date koordinate i obratno.
Zadatak |
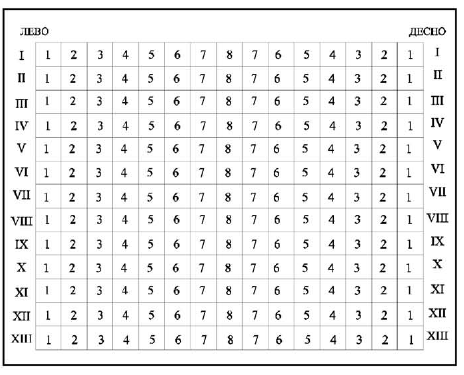
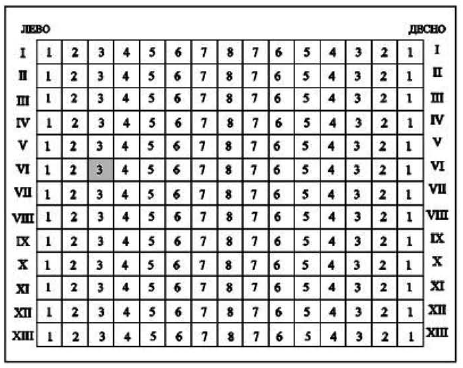
Na slici je prikazan plan bioskopa ODEON, Marko je kupio kartu u šestom redu levo sedište 3. Oboj (osenči) Markovo sedište.
|
Rešenje |
|
MA.1.5.2. Učenik ume da pročita i razume podatak sa grafikona, dijagrama ili iz tabele, i odredi minimum ili maksimum zavisne veličine.
Zadatak |
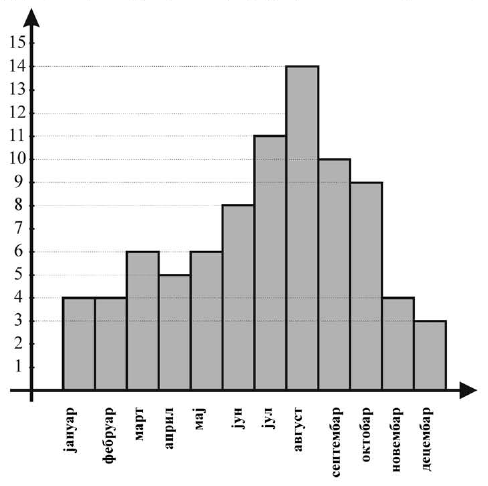
Dijagram prikazuje promene u broju sunčanih dana u godini, po mesecima. |
a) Najmanje sunčanih dana u godini bilo je u mesecu __________. b) Najviše sunčanih dana u godini bilo je u mesecu __________. |
Rešenje |
a) Najmanje sunčanih dana u godini bilo je u mesecu decembru. b) Najviše sunčanih dana u godini bilo je u mesecu avgustu. |
MA.1.5.3. Učenik ume da podatke iz tabele prikaže grafikonom i obrnuto.
Zadatak |
|||||||||||||||
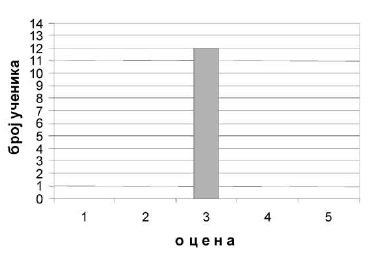
U tabeli je prikazan uspeh učenika na pismenom zadatku.
Na osnovu podataka iz tabele, dovrši grafikon kao što je započeto.
|
|||||||||||||||
Rešenje |
|||||||||||||||
|
|||||||||||||||
MA.1.5.4. Učenik ume da odredi zadati procenat neke veličine.
Zadatak |
Milena je odlučila da kupi patike koje koštaju 4 000 dinara. Prilikom kupovine prodavac joj je odobrio popust od 10%. Koliki je popust u dinarima?
Milena je dobila popust _____ dinara. |
Rešenje |
Milena je dobila popust 400 dinara. |
MA.2.1.1. Učenik ume da uporedi po veličini brojeve zapisane u različitim oblicima.
Zadatak |
|||||||
Dati su brojevi
Koji od datih brojeva je najveći, a koji je najmanji? Najveći broj je _____, a najmanji broj je _____. |
|||||||
Rešenje |
|||||||
Najveći broj je 1½, a najmanji broj je -1,2. |
MA.2.1.2. Učenik ume da odredi suprotan broj, recipročnu vrednost i apsolutnu vrednost broja; izračuna vrednost jednostavnijeg izraza sa više računskih operacija različitog prioriteta, uključujući oslobađanje od zagrada, sa brojevima istog zapisa.
Zadatak |
Izračunaj i napiši odgovarajući rezultat. a) (3/4 - 1/2) · 4 = b) 3,2 · (4,3 + 5,7) =
|
Rešenje |
a) 1 b) 32 |
Zadatak |
||||||||||||||||||
Dopuni sledeću tabelu
|
||||||||||||||||||
Rešenje |
||||||||||||||||||
|
MA.2.1.3. Učenik ume da primeni osnovna pravila deljivosti sa 2, 3, 5, 9 i dekadnim jedinicama.
Zadatak |
||
Poveži date brojeve sa odgovarajućim tvrđenjem.
|
||
Rešenje |
||
Sve tačno povezano; 3030305 povezano sa Broj je deljiv sa 5; 3030302 povezano sa Broj je deljiv sa 2 i 2020203 povezano sa Broj je deljiv sa 3. |
MA.2.1.4. Učenik ume da koristi brojeve i brojevne izraze u jednostavnim realnim situacijama.
Zadatak |
Za 25 svezaka je plaćeno 750 dinara. Sveska je za 20 dinara skuplja od olovke. |
Rešenje |
750:25 = 30 |
MA.2.2.1. Učenik je računske operacije doveo do solidnog stepena uvežbanosti; ume da reši linearne jednačine i sisteme linearnih jednačina sa dve nepoznate.
Zadatak |
|||||||
Zaokruži slovo ispred tačnog odgovora.
a) -20 i -10 b) -10 i 10 v) 10 i 20 g) 20 i 30 |
|||||||
Rešenje |
|||||||
v) 10 i 20 |
MA.2.2.2. Učenik je računske operacije doveo do solidnog stepena uvežbanosti; ume da operiše sa stepenima i zna šta je kvadratni koren.
Zadatak |
|||||||||||||||
Ako je tvrđenje tačno zaokruži reč TAČNO, a ako je netačno zaokruži reč NETAČNO.
|
|||||||||||||||
Rešenje |
|||||||||||||||
Sve tačno zaokruženo. 54 · 53 = 512 zaokruženo NETAČNO; (23)4 = (24)3 zaokruženo TAČNO; 35 : 34 = 3 zaokruženo TAČNO; |
MA.2.2.3. Učenik je računske operacije doveo do solidnog stepena uvežbanosti; ume da sabira i oduzima polinome, ume da pomnoži dva binoma i da kvadrira binom.
Zadatak |
Zaokruži slovo ispred tačnog odgovora. Kvadrat binoma 1/2m - n je: a) 1/2m2 + 2mn + n2 b) 1/4 m2 - mn + n2 v) 1/2 m2 - mn + n2 g) 1/4 m2 - n2 |
Rešenje |
b) 1/4 m2 - mn + n2 |
MA.2.2.4. Učenik je računske operacije doveo do solidnog stepena uvežbanosti; ume da uoči zavisnost među promenljivim, zna funkciju y=ax i grafički interpretira njena svojstva; vezuje za ta svojstva pojam direktne proporcionalnosti i određuje nepoznati član proporcije,
Zadatak |
||||||||
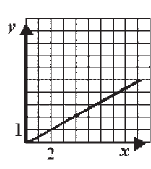
Na jednom od datih crteža grafički je prikazana zavisnost između količine olova (x) i cinka (y) u leguri, u kojoj su olovo i cink zastupljeni u odnosu 2:1.
|
||||||||
Rešenje |
||||||||
|
Zadatak |
Za 8 m platna treba platiti 2 400 dinara. a) Koliko košta 12 m istog platna? b) Koliko se metara istog platna može kupiti za 750 dinara a) 12 m platna košta _____ dinara. b) Za 750 dinara može se kupiti _____ metara platna. |
Rešenje |
a) 12 m platna košta 3 600 dinara. |
MA.2.2.5. Učenik je računske operacije doveo do solidnog stepena uvežbanosti; ume da koristi jednačine u jednostavnim tekstualnim zadacima.
Zadatak |
Kada je Petar potrošio trećinu svoje ušteđevine na kupovinu kredita za mobilni telefon, ostalo mu je 800 dinara. Kolika je bila Petrova ušteđevina? Petrova ušteđevina je bila _____ dinara. |
Rešenje |
Petrova ušteđevina je bila 1200 dinara. |
MA.2.3.1. Učenik ume da odredi suplementne i komplementne uglove, uporedne i unakrsne uglove; računa sa njima ako su izraženi u celim stepenima.
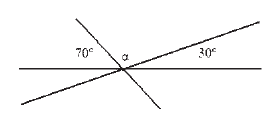
Zadatak |
||
|
||
Rešenje |
||
α = 80° |
MA.2.3.2. Učenik ume da odredi odnos uglova i stranica u trouglu, zbir uglova u trouglu i četvorouglu i da rešava zadatke koristeći Pitagorinu teoremu.
Zadatak |
||
|
||
Rešenje |
||
Površina jedra je 30 m2. |
MA.2.3.3. Učenik ume da koristi formule za obim i površinu kruga i kružnog prstena.
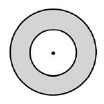
Zadatak |
|||||
|
|||||
Rešenje |
|||||
Poluprečnik većeg kruga je 5 cm. |
|||||
MA.2.3.5. Učenik ume da izračuna površinu i zapreminu valjka, kupe i lopte kada su neophodni elementi neposredno dati u zadatku.
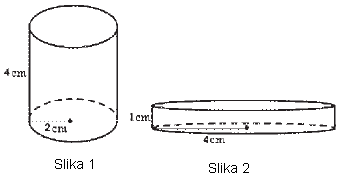
Zadatak |
||||
|
||||
Rešenje |
||||
v) V1 = V2 |
||||
MA.2.3.6. Učenik ume da uoči osnosimetrične figure i da odredi osu simetrije; koristi podudarnost i vezuje je sa karakterističnim svojstvima figura (npr. paralelnost i jednakost stranica paralelograma).
Zadatak |
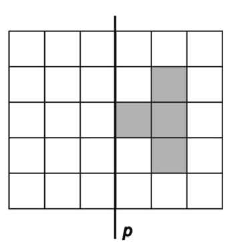
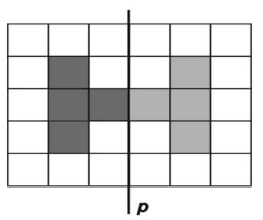
Osenči četiri polja na slici tako da dobiješ figuru simetričnu u odnosu na pravu p. |
|
|
Rešenje |
|
MA.2.4.1. Učenik ume da poredi veličine koje su izražene različitim mernim jedinicama za dužinu i masu.
Zadatak |
|||||||||||||||||||||||||||
Nastavnica je na tabli ispisala mase četiri predmeta.
|
|||||||||||||||||||||||||||
Rešenje |
|||||||||||||||||||||||||||
|
Zadatak |
Prodavac ima u radnji tri očišćena pileta čije su mase 1340 g, 1,35 kg i 1kg 290 g. Poređaj te mase po veličini, od najveće do najmanje.
Odgovor: _____ > _____ > _____ |
Rešenje |
1,35 kg > 1340 g > 1kg 290 g |
MA.2.4.2. Učenik ume da pretvori iznos jedne valute u drugu pravilno postavljajući odgovarajuću proporciju.
Zadatak |
Maja je novogodišnje praznike provela u Italiji. Put i boravak je koštao 200 evra. Koliki iznos je Maja uplatila, u dinarima, ako je na dan uplate 1 evro vredeo 105 dinara?
Maja je uplatila __________ dinara |
Rešenje |
Maja je uplatila 21000 dinara. |
Zadatak |
Ako jedna norveška kruna vredi 12,50 dinara, a jedan evro 105 dinara, koliko vredi 10 evra u norveškim krunama?
10 evra vredi _____ norveških kruna. |
Rešenje |
10 evra je 105 · 10 = 1050 dinara. 1050 : 12,5 = 84 10 evra vredi 84 norveške krune. |
MA.2.4.3. Učenik ume da datu veličinu iskaže približnom vrednošću
Zadatak |
||||||||
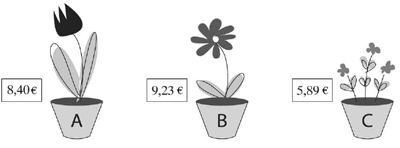
Cvećar treba da zaokrugli cene cveća iz uvoza na najbliži ceo broj. Upiši nove cene.
|
||||||||
Rešenje |
||||||||
|
MA.2.5.1. Učenik vlada opisom koordinatnog sistema (određuje koordinate tačaka, osno ili centralno simetričnih itd).
Zadatak |
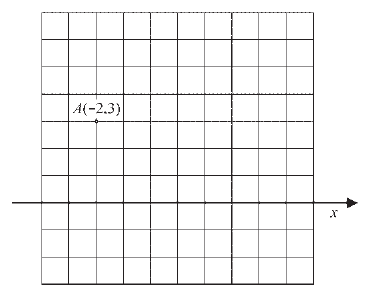
Na osnovu datih koordinata tačke A ucrtaj y osu pravouglog Dekartovog koordinatnog sistema.
|
Rešenje |
|
MA.2.5.2. Učenik ume da čita jednostavne dijagrame i tabele i na osnovu njih obradi podatke po jednom kriterijumu (npr. odredi aritmetičku sredinu za dati skup podataka; poredi vrednosti uzorka sa srednjom vrednošću).
Zadatak |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Data je tabela koja predstavlja međusobna rastojanja gradova izražena u kilometrima.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Na osnovu tabele dopiši sledeće rečenice tako da tvrđenje bude tačno a) Rastojanje između Čačka i Nikšića je __________ kilometara. b) Rastojanje između Nikšića i __________ je isto kao i rastojanje između Nikšića i __________. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Rešenje |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
a) Rastojanje između Čačka i Nikšića je 395 kilometara. b) Rastojanje između Nikšića i Novog Sada je isto kao i |
MA.2.5.3. Učenik ume da obradi prikupljene podatke i predstavi ih tabelarno ili grafički; predstavlja srednju vrednost i medijanu.
Zadatak. |
|||||||||||||||||
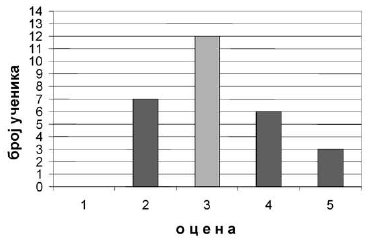
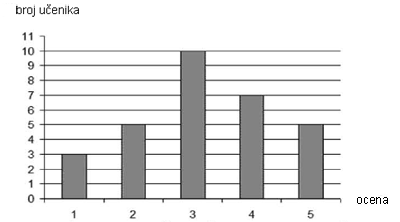
Dijagram prikazuje uspeh učenika jednog odeljenja na testu iz matematike.
a) Dopuni, kao što je započeto, tabelu koja odgovara datom dijagramu:
b) Izračunaj srednju ocenu na testu iz matematike. Srednja ocena na testu iz matematike je _____ |
|||||||||||||||||
Rešenje |
|||||||||||||||||
b) Srednja ocena na testu iz matematike je 3,2 |
|||||||||||||||||
MA.3.1.2. Učenik ume da operiše sa pojmom deljivosti u problemskim situacijama.
Zadatak |
Napiši tri broja pete hiljade čija je cifra desetica 2, a koji su deljivi sa 9.
|
Rešenje |
Napisana bilo koja tri broja iz skupa {4023, 4122, 4221, 4320, 4329, 4428, 4527, 4626, 4725, 4824, 4923}. |
MA.3.1.3. Učenik ume da koristi brojeve i brojevne izraze u realnim situacijama.
Zadatak |
Buketi, koje cvećarka pravi, sadrže 4 ruže i 3 bele rade. Ako cvećarka na svakoj prodatoj ruži zaradi 35 dinara, na svakoj prodatoj beloj radi 25 dinara i na pravljenju buketa 60 dinara, koliko najmanje buketa treba da proda da bi zaradila više od 1500 dinara? Cvećarka treba da proda najmanje _____ buketa. |
Rešenje |
Zarada po jednom buketu: 4 · 35 + 3 · 25 + 60 = 140 + 75 + 60 = 275 |
MA.3.2.2. Učenik je postigao visok stepen uvežbanosti izvođenja operacija uz isticanje svojstava koja se primenjuju; ume da koristi osobine stepena i kvadratnog korena.
Zadatak |
Ako se zna daje 322= 1024, izračunaj a) √10,24 = _______________ b) √102400 = _______________ v) √0,1024 = _______________ |
Rešenje |
a) √10,24 = 3,2 b) √102400 = 320 v) √0,1024 = 0,32 |
MA.3.2.3. Učenik je postigao visok stepen uvežbanosti izvođenja operacija uz isticanje svojstava koja se primenjuju; ume da primenjuje formule za razliku kvadrata i kvadratnog binoma; uvežbano transformiše algebarske izraze i svodi ih na najjednostavniji oblik.
Zadatak |
Zaokruži slovo ispred tačnog odgovora. Polinom (a - 1)(2a + 1) - (a - 6)(a + 6) jednak je polinomu: a) a2 - a + 35 |
Rešenje |
a) a2 - a + 35 |
Zadatak |
Izračunaj i napiši odgovarajući rezultat a) razliku kvadrata brojeva 7 i 3: ____________________________________________________________ b) kvadrat razlike brojeva 7 i 3: _____________________________________________________________ v) zbir kvadrata brojeva 7 i 3: ______________________________________________________________ g) kvadrat zbira brojeva 7 i 3: ______________________________________________________________ |
Rešenje |
a) 72 - 32 = 49 - 9 = 40 b) (7 - 3)2 = 42= 16 v) 72+ 32 = 49 + 9 = 58 g) (7 + 3)2 = 102 = 100 |
MA.3.2.4. Učenik je postigao visok stepen uvežbanosti izvođenja operacija uz isticanje svojstava koja se primenjuju; ume da razlikuje direktno i obrnuto proporcionalne veličine i to izražava odgovarajućim zapisom; zna linearnu funkciju i grafički interpretira njena svojstva.
Zadatak |
||||||||
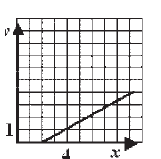
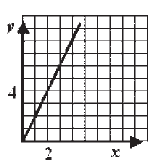
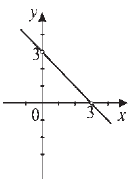
Koji od grafika predstavlja grafik funkcije y = x + 3?
|
||||||||
Rešenje |
||||||||
|
Zadatak |
Devet drugova bi očistili bazen za četiri dana. Koliko još drugova treba da im pomogne da bi bazen bio očišćen za tri dana? Bazen će biti očišćen za tri dana ako im pomognu još _____ druga. |
Rešenje |
Bazen će biti očišćen za tri dana ako im pomognu još 3 druga. |
MA.3.2.5. Učenik je postigao visok stepen uvežbanosti izvođenja operacija uz isticanje svojstava koja se primenjuju: ume da koristi jednačine, nejednačine i sisteme jednačina rešavajući i složenije tekstualne zadatke.
Zadatak |
Dok je bila na letovanju, Nađa se svakom od svojih 9 prijatelja iz zgrade javila ili pismom ili razglednicom. Marke za razglednice je plaćala po 10 dinara a marke za pisma po 15 dinara. Koliko pisama i koliko razglednica je Nađa poslala ako je za marke ukupno potrošila 110 dinara? Nađa je poslala __________ pisama i __________ razglednica. |
Rešenje |
Nađa je poslala 5 pisama i 4 razglednice. |
MA.3.3.1. Učenik ume da računa sa uglovima uključujući i pretvaranje ugaonih mera; zaključuje koristeći osobine paralelnih i normalnih pravih, uključujući uglove na transverzali.
Zadatak |
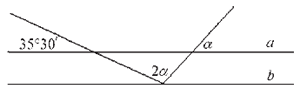
Ako su prave a i b paralelne, odredi koliki je ugao α.
α = _____ |
Rešenje |
Ugao α= 48°10' |
MA.3.3.2. Učenik ume da koristi osnovna svojstva trougla, četvorougla, paralelograma i trapeza, računa njihove obime i površine na osnovu elemenata koji nisu obavezno neposredno dati u formulaciji zadatka; ume da ih konstruiše.
Zadatak |
||
|
||
Rešenje |
||
Potrebno je 48 m žice. |
MA.3.3.3. Učenik ume da odredi centralni i periferijski ugao, računa površinu isečka, kao i dužinu luka.
Zadatak |
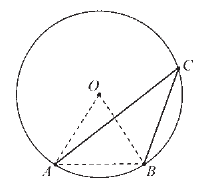
||
Ako je tetiva AB jednaka poluprečniku kruga, izračunaj meru ugla ACB.
|
||
Rešenje |
||
Mera ugla ACB je 30°. |
Zadatak |
Koliko puta je površina kružnog isečka, čiji je centralni ugao 30°, manja od površine kruga? Manja je _____ puta. |
Rešenje |
Manja je 12 puta. |
MA.3.3.4. Učenik ume da izračuna površinu i zapreminu prizme i piramide, uključujući slučajeve kada neophodni elementi nisu neposredno dati.
Zadatak |
||
|
||
Rešenje |
||
Zapremina piramide je 400 cm3. |
MA.3.3.5. Učenik ume da izračuna površinu i zapreminu valjka, kupe i lopte, uključujući slučajeve kada neophodni elementi nisu neposredno dati.
Zadatak |
Pravougli trougao, čije su katete a = 9 cm, b = 12 cm, rotira oko katete b. Koliki je odnos između površine osnove i površine omotača dobijene kupe? Zaokruži slovo ispred tačnog odgovora. a) 1: 1 b) 3 : 4 v) 3 : 5 g) 4 : 5 |
Rešenje |
v) 3:5 |
Zadatak |
Kolika je površina najveće lopte koja može da stane u kutiju oblika kocke ivice 20 cm? Površina lopte je ___ cm2. |
Rešenje |
Površina lopte je 400π cm2. |
MA.3.3.6. Učenik ume da primeni podudarnost i sličnost trouglova, povezujući tako razna svojstva geometrijskih objekata.
Zadatak |
|||
|
|
||
Rešenje |
|||
a) 2 : 1 |
|||
Zadatak |
||||||||||||
Kod tačnog tvrđenja zaokruži reč Tačno, a kod netačnog tvrđenja reč Netačno. |
||||||||||||
|
||||||||||||
Rešenje |
||||||||||||
Sve tačno zaokruženo. Svaka dva jednakostranična trougla međusobno su slična - zaokruženo TAČNO; Svaka dva slična trougla imaju jednake obime - zaokruženo NETAČNO; Dva jednakokraka trougla sa uglom pri vrhu od 36° su slični trouglovi - zaokruženo TAČNO; Svi pravougli trouglovi međusobno su slični - zaokruženo NETAČNO. |
MA.3.4.2. Učenik ume da proceni i zaokrugli date podatke i računa sa takvim približnim vrednostima; izražava ocenu greške (npr. manje od 1 dinar, 1cm, 1 g).
Zadatak |
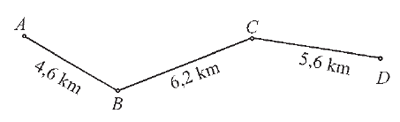
Rastojanje između mesta A i mesta D prikazano je na sledećoj mapi.
Mira je procenila rastojanje između mesta A i mesta D tako što je zaokruglila svako od rastojanja na najbliži ceo broj kilometara i sabrala ih. Vera je sabrala rastojanja naznačena na mapi, i dobijeni rezultat zaokruglila na najbliži ceo broj kilometara. Zaokruži slovo ispred tačnog odgovora. a) Mira je dobila veći broj od Vere. |
Rešenje |
a) Mira je dobila veći broj od Vere. |
MA.3.5.1. Učenik ume da odredi položaj (koordinate) tačaka koje zadovoljavaju složenije uslove.
Zadatak |
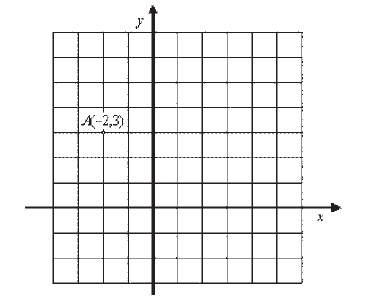
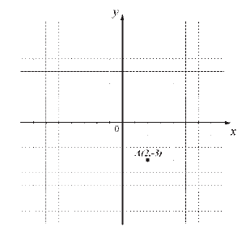
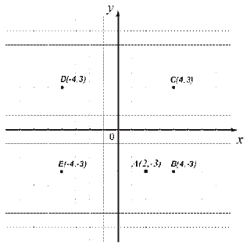
Ucrtaj u koordinatni sistem sve tačke koje su na istom rastojanju od x ose kao i tačka A, a kojima je rastojanje od y ose dva puta veće nego rastojanje tačke A od y ose.
|
Rešenje |
|
|
MA.3.5.2. Učenik ume da tumači dijagrame i tabele
Zadatak |
||||||||||||||||||||||||||||||||||||||||||||||||
U tabeli su data rastojanja nekih gradova u kilometrima.
a) Koji grad je od Beograda udaljen 115 km? _______________ b) Koja dva grada su udaljena 353 km? ____________________ v) Koja dva grada su udaljena manje od 50 km? ____________________ g) Koliko gradova u tabeli je od Beograda udaljeno više od 200 km? _____ |
||||||||||||||||||||||||||||||||||||||||||||||||
Rešenje |
||||||||||||||||||||||||||||||||||||||||||||||||
a) Kragujevac b) Kraljevo i Subotica v) Jagodina i Kragujevac g) tri |
MA.3.5.3. Učenik ume da prikupi i obradi podatke i sam sastavi dijagram ili tabelu; crta grafik kojim predstavlja međuzavisnost veličina.
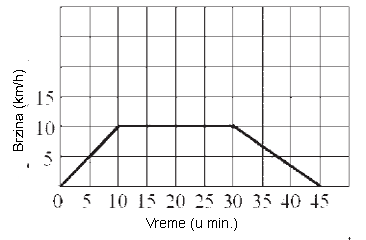
Zadatak |
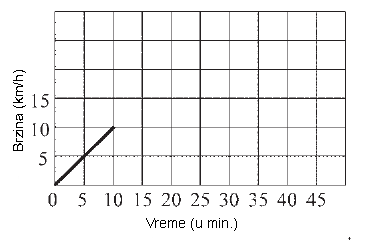
Maja je vozila bicikl 45 minuta. Posle prvih 10 minuta vožnje dostigla je brzinu od 10 km/h. Vozila je tom brzinom narednih 20 minuta, a zatim počela da ravnomerno usporava dok se nije zaustavila. Dopuni dijagram koji prikazuje Majinu vožnju, kao što je započeto.
|
Rešenje |
|
MA.3.5.4. Učenik ume da primeni procentni račun u složenijim situacijama.
Zadatak |
Cena knjige je prvo povećana za 10%, a zatim je smanjena za 10% i sada iznosi 198 dinara. Kolika je bila cena knjige pre poskupljenja? Zaokruži slovo ispred tačnog odgovora. a) 198 dinara b) 200 dinara v) 202 dinara g) 196,02 dinara |
Rešenje |
b) 200 dinara |
Obrazovni standardi za kraj obaveznog obrazovanja za matematiku koji će biti ispitani nepoznatim zadacima
MA.2.3.4. Učenik ume da vlada pojmovima: prizma i piramida; računa njihovu površinu i zapreminu kada su neophodni elementi neposredno dati u zadatku.
Zadatak |
Ivica pravilne trostrane jednakoivične piramide je 8 cm. Kolika je njena površina? Površina piramide je _____ cm2. |
Rešenje |
Površina piramide je 64√3cm2. |
MA.2.5.4. Učenik ume da primeni procentni račun u jednostavnim realnim situacijama (na primer, promena cene nekog proizvoda za dati procenat).
Zadatak |
Gordana prodaje sladoled. Za svaki prodati sladoled po ceni od 60 dinara, ona zarađuje 6 dinara. Kolika je njena zarada po jednom sladoledu izražena u procentima? a) 6 % b) 1 % v) 54 % g) 10% |
Rešenje |
g) 10% |
MA.3.1.1. Učenik ume da odredi vrednost složenijeg brojevnog izraza.
Zadatak |
Izračunaj proizvod izraza A i B, ako je A = 1 + 3 : 6/5 - 2/5 · 5/4 i B = 8/3 - 7/3 · 6/7. A = _____, B = _____, A · B = _____ |
Rešenje |
A = 3, B = 2/3, A · B = 2 |
MA.3.2.1. Učenik je postigao visok stepen uvežbanosti izvođenja operacija uz isticanje svojstava koja se primenjuju; ume da sastavlja i rešava linearne jednačine i nejednačine i sisteme linearnih jednačina sa dve nepoznate.
Zadatak |
||||
Zaokruži slovo ispred tačnog odgovora.
|
||||
Rešenje |
||||
|
MA.3.4.1. Učenik ume da po potrebi pretvara jedinice mere, računajući sa njima.
Zadatak |
Film se završio u 22 časa i 10 minuta. Kada je film počeo ako je trajao 115 minuta? Zaokruži slovo ispred tačnog odgovora. a) 20 časova i 55 minuta b) 20 časova i 45 minuta v) 20 časova i 15 minuta g) 20 časova i 5 minuta |
Rešenje |
v) 20 časova 15 minuta |